【题目】(1)如图①,直线AB∥CD,E是AB与AD之间的一点,连接BE,CE,可以发现∠B+∠C=∠BEC.

证明过程如下:
证明:过点E作EF∥AB,
∵AB∥DC,EF∥AB(辅助线的作法),
∴EF∥DC
∴∠C=∠CEF.
∵EF∥AB,∴∠B=∠BEF
∴∠B+∠C=∠CEF+∠BEF
即∠B+∠C=∠BEC.
(2)如果点E运动到图②所示的位置,其他条件不变,∠B,∠C,∠BEC又有什么关系?并证明你的结论;
(3)如图③,AB∥DC,∠C=120°,∠AEC=80°,则∠A= .(写出结论,不用写计算过程)。
参考答案:
【答案】(2)∠B+∠C=360°﹣∠BEC;证明见解析;(3)20°.
【解析】(1)(2)(3)分别过E作EF∥AB,根据平行线的判定得出AB∥CD∥EF,根据平行线的性质得出即可.
(2)证明:如图②,过点E作EF∥AB,

∵AB∥DC(已知),EF∥AB(辅助线的作法),
∴EF∥DC(平行于同一直线的两直线平行),
∴∠C+∠CEF=180°,∠B+∠BEF=180°,
∴∠B+∠C+∠AEC=360°,
∴∠B+∠C=360°﹣∠BEC;
(3)解:如图③,过点E作EF∥AB,

∵AB∥DC(已知),EF∥AB(辅助线的作法),
∴EF∥DC(平行于同一直线的两直线平行),
∴∠C+∠CEF=180°,∠A=∠BEF,
∵∠C=120°,∠AEC=80°,
∴∠CEF=180°﹣120°=60°,
∴∠BEF=80°﹣60°=20°,
∴∠A=∠BEF=20°.
故答案为:20°.
“点睛”本题考查了平行线的性质和判定的应用,能正确作出辅助线是解题的关键,注意:(1)两直线平行,内错角相等;(2)两直线平行,同位角相等;(3)两直线平行,同旁内角互补,以及平行于同一直线的两直线平行的运用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面计算
 +
+ +
+ +…+
+…+ 的过程,然后填空.
的过程,然后填空.解:∵
 =
= (
( -
- ),
), =
= (
( -
- ),…,
),…, =
= (
( -
- ),
),∴
 +
+ +
+ +…+
+…+
=
 (
( -
- )+
)+ (
( -
- )+
)+ (
( -
- )+…+
)+…+ (
( -
- )
)=
 (
( -
- +
+ -
- +
+ -
- +…+
+…+ -
- )
)=
 (
( -
- )
)=
 .
.以上方法为裂项求和法,请参考以上做法完成:
(1)
 +
+ =______;
=______;(2)当
 +
+ +
+ +…+x=
+…+x= 时,最后一项x=______.
时,最后一项x=______. -
科目: 来源: 题型:
查看答案和解析>>【题目】一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲、乙两组工作一天,商店各应付多少钱?
(2)已知甲组单独完成需12天,乙组单独完成需24天,单独请哪个组,商店所需费用
较少?
(3)若装修完后,商店每天可赢利200元,现有三种方案:①甲组单独做;②乙组单独做;③甲、乙两组同时做.你认为哪一种施工方案更有利于商店?请你帮商店做出决策(可用(1)(2)问中的条件及结论).
-
科目: 来源: 题型:
查看答案和解析>>【题目】当我们利用两种不同的方法计算同一图形的面积时,可以得到一个等式.例如,由图①,可得等式:(a+2b)(a+b)=a2+3ab+2b2.
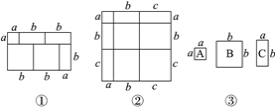
(1)由图②,写出所得的等式;
(2)利用(1)中所得到的结论,解决下面的问题: 已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)如图③,琪琪用2 张A型纸片,3 张B型纸片,5 张C型纸片拼出一个长方形,那么该长方形较长的一条边长为多少.(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
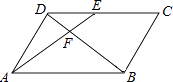
A.2:5
B.2:3
C.3:5
D.3:2 -
科目: 来源: 题型:
查看答案和解析>>【题目】若抛物线y=x2﹣2x+c与y轴的交点为(0,﹣3),则下列说法不正确的是( )
A.抛物线开口向上
B.抛物线的对称轴是x=1
C.当x=1时,y的最大值为﹣4
D.抛物线与x轴的交点为(﹣1,0),(3,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】下面是老师在嘉嘉的数学作业本上截取的部分内容:

问题:(1)这种解方程组的方法叫什么方法;嘉嘉的解法正确吗?如果不正确,从哪一步开始出错的?请你指出错误的原因,并求出正确的解.
(2)请用不同于(1)中的方法解这个方程组.
相关试题

