【题目】若抛物线y=x2﹣2x+c与y轴的交点为(0,﹣3),则下列说法不正确的是( )
A.抛物线开口向上
B.抛物线的对称轴是x=1
C.当x=1时,y的最大值为﹣4
D.抛物线与x轴的交点为(﹣1,0),(3,0)
参考答案:
【答案】C
【解析】解:∵抛物线过点(0,﹣3), ∴抛物线的解析式为:y=x2﹣2x﹣3.
A、抛物线的二次项系数为1>0,抛物线的开口向上,正确.
B、根据抛物线的对称轴x=﹣ ![]() =﹣
=﹣ ![]() =1,正确.
=1,正确.
C、由A知抛物线的开口向上,二次函数有最小值,当x=1时,y的最小值为﹣4,而不是最大值.故本选项错误.
D、当y=0时,有x2﹣2x﹣3=0,解得:x1=﹣1,x2=3,抛物线与x轴的交点坐标为(﹣1,0),(3,0).正确.
故选C.
【考点精析】认真审题,首先需要了解二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小).
-
科目: 来源: 题型:
查看答案和解析>>【题目】当我们利用两种不同的方法计算同一图形的面积时,可以得到一个等式.例如,由图①,可得等式:(a+2b)(a+b)=a2+3ab+2b2.
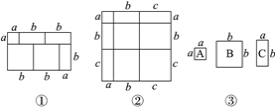
(1)由图②,写出所得的等式;
(2)利用(1)中所得到的结论,解决下面的问题: 已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)如图③,琪琪用2 张A型纸片,3 张B型纸片,5 张C型纸片拼出一个长方形,那么该长方形较长的一条边长为多少.(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,直线AB∥CD,E是AB与AD之间的一点,连接BE,CE,可以发现∠B+∠C=∠BEC.

证明过程如下:
证明:过点E作EF∥AB,
∵AB∥DC,EF∥AB(辅助线的作法),
∴EF∥DC
∴∠C=∠CEF.
∵EF∥AB,∴∠B=∠BEF
∴∠B+∠C=∠CEF+∠BEF
即∠B+∠C=∠BEC.
(2)如果点E运动到图②所示的位置,其他条件不变,∠B,∠C,∠BEC又有什么关系?并证明你的结论;
(3)如图③,AB∥DC,∠C=120°,∠AEC=80°,则∠A= .(写出结论,不用写计算过程)。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
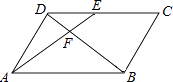
A.2:5
B.2:3
C.3:5
D.3:2 -
科目: 来源: 题型:
查看答案和解析>>【题目】下面是老师在嘉嘉的数学作业本上截取的部分内容:

问题:(1)这种解方程组的方法叫什么方法;嘉嘉的解法正确吗?如果不正确,从哪一步开始出错的?请你指出错误的原因,并求出正确的解.
(2)请用不同于(1)中的方法解这个方程组.
-
科目: 来源: 题型:
查看答案和解析>>【题目】同时抛掷A、B两个均匀的小立方体(每个面上分别标有数字1,2,3,4,5,6),设两立方体朝上的数字分别为x、y,并以此确定点P(x,y),那么点P落在抛物线y=﹣x2+3x上的概率为( )
A.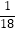
B.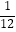
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数
 (x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( )
(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( ) 
A.1
B.2
C.3
D.4
相关试题

