搜索
【题目】下面是老师在嘉嘉的数学作业本上截取的部分内容：
问题：(1)这种解方程组的方法叫什么方法；嘉嘉的解法正确吗？如果不正确，从哪一步开始出错的？请你指出错误的原因，并求出正确的解．
(2)请用不同于(1)中的方法解这个方程组．
参考答案：
【答案】(1)代入消元法，不正确，从第二步开始出错的，
；(2) 请用不同于(1)中的方法解这个方程组见解析.
【解析】
根据解方程组的基本步骤一一作答.
(1)代入消元法，不正确，从第二步开始出错的，不能把方程③代入方程①.正确解法如下：
由方程①，得y＝2x－3.③
将③代入②，得x＋(2x－3)＝－12，
解得x＝－3.
把x＝－3代入③，得y＝－9.
所以原方程组的解为
(2)①＋②，得3x＝－9，解得x＝－3.
把x＝－3代入②，得y＝－9.
所以原方程组的解为
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图①，直线AB∥CD，E是AB与AD之间的一点，连接BE，CE，可以发现∠B+∠C=∠BEC．
证明过程如下：
证明：过点E作EF∥AB，
∵AB∥DC，EF∥AB（辅助线的作法），
∴EF∥DC
∴∠C=∠CEF．
∵EF∥AB，∴∠B=∠BEF
∴∠B+∠C=∠CEF+∠BEF
即∠B+∠C=∠BEC．
（2）如果点E运动到图②所示的位置，其他条件不变，∠B，∠C，∠BEC又有什么关系？并证明你的结论；
（3）如图③，AB∥DC，∠C=120°，∠AEC=80°，则∠A= ．（写出结论，不用写计算过程）。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在ABCD中，E为CD上一点，连接AE、BD，且AE、BD交于点F，S△DEF：S△ABF=4：25，则DE：EC=（ ）
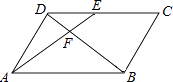
A.2：5
B.2：3
C.3：5
D.3：2 -
科目： 来源： 题型：
查看答案和解析>>【题目】若抛物线y=x2﹣2x+c与y轴的交点为（0，﹣3），则下列说法不正确的是（ ）
A.抛物线开口向上
B.抛物线的对称轴是x=1
C.当x=1时，y的最大值为﹣4
D.抛物线与x轴的交点为（﹣1，0），（3，0） -
科目： 来源： 题型：
查看答案和解析>>【题目】同时抛掷A、B两个均匀的小立方体（每个面上分别标有数字1，2，3，4，5，6），设两立方体朝上的数字分别为x、y，并以此确定点P（x，y），那么点P落在抛物线y=﹣x2+3x上的概率为（ ）
A.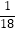
B.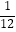
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，反比例函数
（x＞0）的图象经过矩形OABC对角线的交点M，分别与AB、BC交于点D、E，若四边形ODBE的面积为9，则k的值为（ ） 
A.1
B.2
C.3
D.4 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：关于x的一元二次方程x2﹣（2m+3）x+m2+3m+2=0．
（1）已知x=2是方程的一个根，求m的值；
（2）以这个方程的两个实数根作为△ABC中AB、AC（AB＜AC）的边长，当BC=
时，△ABC是等腰三角形，求此时m的值.
相关试题
