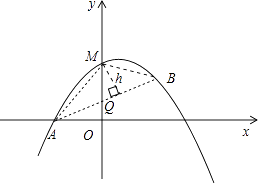
【题目】如图,已知抛物线y=ax2+bx+1经过A(﹣1,0),B(1,1)两点.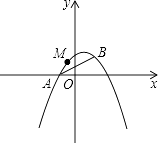
(1)求该抛物线的解析式;
(2)阅读理解:
在同一平面直角坐标系中,直线l1:y=k1x+b1(k1 , b1为常数,且k1≠0),直线l2:y=k2x+b2(k2 , b2为常数,且k2≠0),若l1⊥l2 , 则k1k2=﹣1.
解决问题:
①若直线y=3x﹣1与直线y=mx+2互相垂直,求m的值;
②抛物线上是否存在点P,使得△PAB是以AB为直角边的直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)M是抛物线上一动点,且在直线AB的上方(不与A,B重合),求点M到直线AB的距离的最大值.
参考答案:
【答案】
(1)解:将A,B点坐标代入,得
![]() ,
,
解得 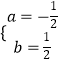 ,
,
抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x+1;
x+1;
(2)解:①由直线y=3x﹣1与直线y=mx+2互相垂直,得
3m=﹣1,
即m=﹣ ![]() ;
;
②AB的解析式为y= ![]() x+
x+ ![]() ,
,
当PA⊥AB时,PA的解析式为y=﹣2x﹣2,
联立PA与抛物线,得
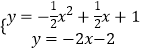 ,
,
解得 ![]() (舍),
(舍), ![]() ,即P(6,﹣14);
,即P(6,﹣14);
当PB⊥AB时,PB的解析式为y=﹣2x+3,
联立PB与抛物线,得 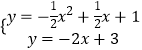 ,
,
解得 ![]() (舍)
(舍) ![]() 即P(4,﹣5),
即P(4,﹣5),
综上所述:△PAB是以AB为直角边的直角三角形,点P的坐标(6,﹣14)(4,﹣5);
(3)解:如图
 ,
,
∵M(t,﹣ ![]() t2+
t2+ ![]() t+1),Q(t,
t+1),Q(t, ![]() t+
t+ ![]() ),
),
∴MQ=﹣ ![]() t2+
t2+ ![]()
S△MAB= ![]() MQ|xB﹣xA
MQ|xB﹣xA
= ![]() (﹣
(﹣ ![]() t2+
t2+ ![]() )×2
)×2
=﹣ ![]() t2+
t2+ ![]() ,
,
当t=0时,S取最大值 ![]() ,即M(0,1).
,即M(0,1).
由勾股定理,得
AB= ![]() =
= ![]() ,
,
设M到AB的距离为h,由三角形的面积,得
h= ![]() =
= ![]() .
.
点M到直线AB的距离的最大值是 ![]() .
.
【解析】(1)利用待定系数法把A、B两点的坐标代入解析式即可求出a、b;(2)分类讨论,A或B为直角顶点两类,利用“阅读理解”的结论“相互垂直的直线的斜率k 乘积=-1”构建方程,求出直线解析式,再和抛物线联立方程组,得出交点即P坐标;(3)三角形的底边AB是定值,要求距离最大值就须求面积的最大值,须过M点作x轴的垂线,把三角形MAB分割成两个有竖直边的三角形,构建以M的横坐标t 为自变量的函数S,求出其最大值,再利用三角形面积公式,求出此时的点M到AB的距离,就是最大距离.
【考点精析】根据题目的已知条件,利用二次函数的最值的相关知识可以得到问题的答案,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.

(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD= ,求
,求  的值.
的值.
(3)在(2)的条件下,设⊙O的半径为3,求AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙M与菱形ABCD在平面直角坐标系中,点M的坐标为(﹣3,1),点A的坐标为(2,0),点B的坐标为(1,﹣
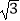 ),点D在x轴上,且点D在点A的右侧.
),点D在x轴上,且点D在点A的右侧.
(1)求菱形ABCD的周长;
(2)若⊙M沿x轴向右以每秒2个单位长度的速度平移,菱形ABCD沿x轴向左以每秒3个单位长度的速度平移,设菱形移动的时间为t(秒),当⊙M与AD相切,且切点为AD的中点时,连接AC,求t的值及∠MAC的度数;
(3)在(2)的条件下,当点M与AC所在的直线的距离为1时,求t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备五一组织老师去隆中参加诸葛亮文化节,现有甲、乙两家旅行社表示对老师优惠,设参加文化节的老师有x人,甲、乙两家旅行社实际收费为y1、y2,且它们的函数图象如图所示,根据图象信息,请你回答下列问题:
(1)当参加老师的人数为多少时,两家旅行社收费相同?
(2)求出y1、y2关于x的函数关系式?
(3)如果共有50人参加时,选择哪家旅行社合算?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直线l与x轴、y轴分别交于点B(4,0)、C(0,3),点A为x轴负半轴上一点,AM⊥BC于点M交y轴于点N(0,
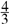 ).已知抛物线y=ax2+bx+c经过点A,B,C.
).已知抛物线y=ax2+bx+c经过点A,B,C.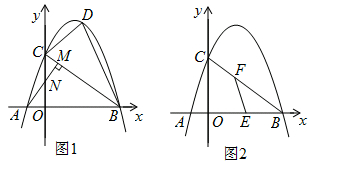
(1)求抛物线的函数式.
(2)连接AC,点D在线段BC上方的抛物线上,连接DC,DB,若△BCD和△ABC面积满足S△BCD=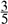 S△ABC , 求点D的坐标.
S△ABC , 求点D的坐标.
(3)如图2,E为OB中点,设F为线段BC上一点(不含端点),连接EF.一动点P从E出发,沿线段EF以每秒3个单位的速度运动到F,再沿着线段PC以每秒5个单位的速度运动到C后停止.若点P在整个运动过程中用时最少,请直接写出最少时间和此时点F的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“小组合作制”正在七年级如火如茶地开展,旨在培养七年级学生的合作学习的精神和能力,学会在合作中自主探索.数学课上,吴老师在讲授“角平分线”时,设计了如下四种教学方法:①教师讲授,学生练习;②学生合作交流,探索规律;③教师引导学生总结规律,学生练习;④教师引导学生总结规律,学生合作交流,吴老师将上述教学方法作为调研内容发到七年级所有同学手中要求每位同学选出自己最喜欢的一种,然后吴老师从所有调查问卷中随机抽取了若干份调查问卷作为样本,统计如下:
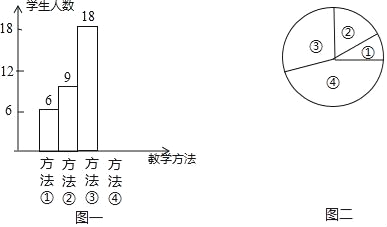
序号①②③④代表上述四种教学方法,图二中,表示①部分的扇形的中心角度数为36°,请回答问题:
(1)在后来的抽样调查中,吴老师共抽取 位学生进行调查;并将条形统计图补充完整;
(2)图二中,表示③部分的扇形的中心角为多少度?
(3)若七年级学生中选择④种教学方法的有540人,请估计七年级总人数约为多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,BC=6.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )

A.2
B.3
C.
D.
相关试题

