【题目】“小组合作制”正在七年级如火如茶地开展,旨在培养七年级学生的合作学习的精神和能力,学会在合作中自主探索.数学课上,吴老师在讲授“角平分线”时,设计了如下四种教学方法:①教师讲授,学生练习;②学生合作交流,探索规律;③教师引导学生总结规律,学生练习;④教师引导学生总结规律,学生合作交流,吴老师将上述教学方法作为调研内容发到七年级所有同学手中要求每位同学选出自己最喜欢的一种,然后吴老师从所有调查问卷中随机抽取了若干份调查问卷作为样本,统计如下:
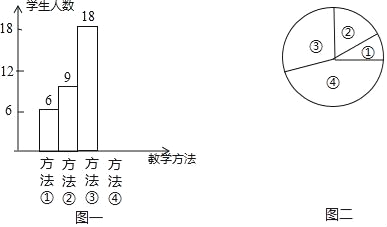
序号①②③④代表上述四种教学方法,图二中,表示①部分的扇形的中心角度数为36°,请回答问题:
(1)在后来的抽样调查中,吴老师共抽取 位学生进行调查;并将条形统计图补充完整;
(2)图二中,表示③部分的扇形的中心角为多少度?
(3)若七年级学生中选择④种教学方法的有540人,请估计七年级总人数约为多少人?
参考答案:
【答案】(1)60,图形见解析;(2)108°;(3)1200人
【解析】
(1)根据样本总量与频数之间的关系求出总人数,根据总人数补全图形;
(2)看图可知③人数为18,故③部分的扇形的中心角为360°×![]() =108°;
=108°;
(3)由题意可求出:七年级总人数=540÷![]() ,从而求出答案.
,从而求出答案.
(1)吴老师抽取的学生总人数为6÷![]() =60人,
=60人,
则方法④的人数为60﹣(6+9+18)=27人,
补全图形如下:

故答案为:60;
(2)表示③部分的扇形的中心角为360°×![]() =108°;
=108°;
(3)估计七年级总人数约为540÷![]() =1200(人).
=1200(人).
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备五一组织老师去隆中参加诸葛亮文化节,现有甲、乙两家旅行社表示对老师优惠,设参加文化节的老师有x人,甲、乙两家旅行社实际收费为y1、y2,且它们的函数图象如图所示,根据图象信息,请你回答下列问题:
(1)当参加老师的人数为多少时,两家旅行社收费相同?
(2)求出y1、y2关于x的函数关系式?
(3)如果共有50人参加时,选择哪家旅行社合算?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+1经过A(﹣1,0),B(1,1)两点.
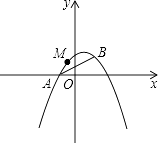
(1)求该抛物线的解析式;
(2)阅读理解:
在同一平面直角坐标系中,直线l1:y=k1x+b1(k1 , b1为常数,且k1≠0),直线l2:y=k2x+b2(k2 , b2为常数,且k2≠0),若l1⊥l2 , 则k1k2=﹣1.
解决问题:
①若直线y=3x﹣1与直线y=mx+2互相垂直,求m的值;
②抛物线上是否存在点P,使得△PAB是以AB为直角边的直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)M是抛物线上一动点,且在直线AB的上方(不与A,B重合),求点M到直线AB的距离的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直线l与x轴、y轴分别交于点B(4,0)、C(0,3),点A为x轴负半轴上一点,AM⊥BC于点M交y轴于点N(0,
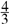 ).已知抛物线y=ax2+bx+c经过点A,B,C.
).已知抛物线y=ax2+bx+c经过点A,B,C.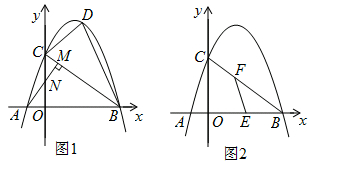
(1)求抛物线的函数式.
(2)连接AC,点D在线段BC上方的抛物线上,连接DC,DB,若△BCD和△ABC面积满足S△BCD=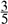 S△ABC , 求点D的坐标.
S△ABC , 求点D的坐标.
(3)如图2,E为OB中点,设F为线段BC上一点(不含端点),连接EF.一动点P从E出发,沿线段EF以每秒3个单位的速度运动到F,再沿着线段PC以每秒5个单位的速度运动到C后停止.若点P在整个运动过程中用时最少,请直接写出最少时间和此时点F的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,BC=6.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )

A.2
B.3
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场元旦期间对所有商品进行优惠促销优惠方案是:一次性购商品不超过1000元,不享受优惠;一次性购商品超过1000元但不超过2000元一律打九折;一次性购商品2000元以上一律打八折.
 如果小明一次性购商品的原价为2500元,那么他实际付款______元
如果小明一次性购商品的原价为2500元,那么他实际付款______元
 如果小华同学一次性购商品付款1620元,那么小华所购商品的原价为多少元?
如果小华同学一次性购商品付款1620元,那么小华所购商品的原价为多少元? -
科目: 来源: 题型:
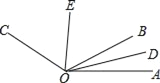
查看答案和解析>>【题目】如图,OD是∠AOB的平分线,OE是∠BOC的平分线.
(1)若∠BOC=50°,∠BOA=80°,求∠DOE的度数;
(2)若∠AOC=150°,求∠DOE的度数;
(3)你发现∠DOE与∠AOC有什么等量关系?给出结论并说明.
相关试题

