【题目】如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD= ![]() ,求
,求 ![]() 的值.
的值.
(3)在(2)的条件下,设⊙O的半径为3,求AB的长.
参考答案:
【答案】
(1)证明:如图,过点O作OF⊥AB于点F,
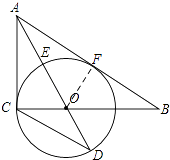
∵AO平分∠CAB,
OC⊥AC,OF⊥AB,
∴OC=OF,
∴AB是⊙O的切线;
(2)解:如图,连接CE,
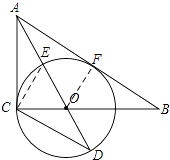
∵ED是⊙O的直径,
∴∠ECD=90°,
∴∠ECO+∠OCD=90°,
∵∠ACB=90°,
∴∠ACE+∠ECO=90°,
∴∠ACE=∠OCD,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠ACE=∠ODC,
∵∠CAE=∠CAE,
∴△ACE∽△ADC,
∴ ![]() ,
,
∵tan∠D= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]()
(3)解:由(2)可知: ![]() =
= ![]() ,
,
∴设AE=x,AC=2x,
∵△ACE∽△ADC,
∴ ![]() ,
,
∴AC2=AEAD,
∴(2x)2=x(x+6),
解得:x=2或x=0(不合题意,舍去),
∴AE=2,AC=4,
由(1)可知:AC=AF=4,
∠OFB=∠ACB=90°,
∵∠B=∠B,
∴△OFB∽△ACB,
∴ ![]() =
= ![]() ,
,
设BF=a,
∴BC= ![]() ,
,
∴BO=BC﹣OC= ![]() ﹣3,
﹣3,
在Rt△BOF中,
BO2=OF2+BF2,
∴( ![]() ﹣3)2=32+a2,
﹣3)2=32+a2,
∴解得:a= ![]() 或a=0(不合题意,舍去),
或a=0(不合题意,舍去),
∴AB=AF+BF= ![]() .
.
【解析】(1)证AB是⊙O的切线,需要证明AB垂直半径,为此过点O作OF⊥AB于点F,再证明OF是半径可得证;
(2)连接CE,先证明△ACE∽△ADC,从而利用相似三角形的对应边成比例得到![]() ,再由tan∠D的值可求得答案;
,再由tan∠D的值可求得答案;
(3)由△ACE∽△ADC,再利用相似三角形的对应边成比例得到AE、AC的长,设BF=a,再证明△OFB∽△ACB,利用相似三角形的对应边成比例可用a表示出BO,在Rt△BOF中,由勾股定理可求出a的值,进而求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某书店老板去图书批发市场购买某种图书,第一次用1200元购书若干本,并按该书定价7元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用1500元所购该书的数量比第一次多10本,当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书.
(1)第一次购书的进价是多少元?
(2)试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其他因素)?若赔钱,赔多少;若赚钱,赚多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市规定:出租车起步价允许行驶的最远路程为3千米,超过3千米的部分按每千米另行收费,甲说:“我乘这种出租车走了9千米,付了15元”:乙说:“我乘这种出租车走了25千米,付了39元”请你算一算这种出租车的起步价是多少元?超过3千米后,每千米的车费是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数
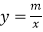 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△AOB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙M与菱形ABCD在平面直角坐标系中,点M的坐标为(﹣3,1),点A的坐标为(2,0),点B的坐标为(1,﹣
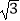 ),点D在x轴上,且点D在点A的右侧.
),点D在x轴上,且点D在点A的右侧.
(1)求菱形ABCD的周长;
(2)若⊙M沿x轴向右以每秒2个单位长度的速度平移,菱形ABCD沿x轴向左以每秒3个单位长度的速度平移,设菱形移动的时间为t(秒),当⊙M与AD相切,且切点为AD的中点时,连接AC,求t的值及∠MAC的度数;
(3)在(2)的条件下,当点M与AC所在的直线的距离为1时,求t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备五一组织老师去隆中参加诸葛亮文化节,现有甲、乙两家旅行社表示对老师优惠,设参加文化节的老师有x人,甲、乙两家旅行社实际收费为y1、y2,且它们的函数图象如图所示,根据图象信息,请你回答下列问题:
(1)当参加老师的人数为多少时,两家旅行社收费相同?
(2)求出y1、y2关于x的函数关系式?
(3)如果共有50人参加时,选择哪家旅行社合算?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+1经过A(﹣1,0),B(1,1)两点.
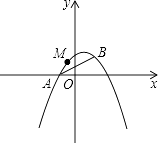
(1)求该抛物线的解析式;
(2)阅读理解:
在同一平面直角坐标系中,直线l1:y=k1x+b1(k1 , b1为常数,且k1≠0),直线l2:y=k2x+b2(k2 , b2为常数,且k2≠0),若l1⊥l2 , 则k1k2=﹣1.
解决问题:
①若直线y=3x﹣1与直线y=mx+2互相垂直,求m的值;
②抛物线上是否存在点P,使得△PAB是以AB为直角边的直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)M是抛物线上一动点,且在直线AB的上方(不与A,B重合),求点M到直线AB的距离的最大值.
相关试题

