搜索
【题目】如图，小红做了一个实验，将正六边形ABCDEF绕点F顺时针旋转后到达A′B′C′D′E′F′的位置，所转过的度数是（ ）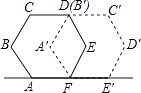 
A.60°
B.72°
C.108°
D.120°
参考答案：
【答案】A
【解析】解：∵六边形ABCDEF是正六边形， ∴∠AFE= 
=120°，
∴∠EFE′=180°﹣∠AFE=180°﹣120°=60°，
∵将正六边形ABCDEF绕点F顺时针旋转后到达A′B′C′D′E′F′的位置，
∴∠EFE′是旋转角，
∴所转过的度数是60°．
故选A．
【考点精析】本题主要考查了正多边形和圆和旋转的性质的相关知识点，需要掌握圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角；圆的外切四边形的两组对边的和相等；①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的直径，AC是弦，直线EF经过点C，AD⊥EF于点D，∠DAC=∠BAC．
（1）求证：EF是⊙O的切线；
（2）求证：AC2=ADAB；
（3）若⊙O的半径为2，∠ACD=30°，求图中阴影部分的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图甲，在平面直角坐标系中，A、B的坐标分别为（4，0）、（0，3），抛物线y=
x2+bx+c经过点B，且对称轴是直线x=﹣ 
．
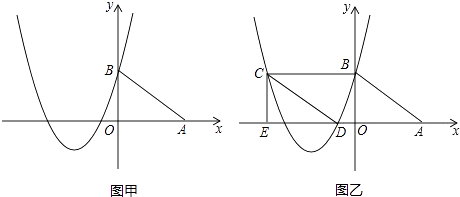
（1）求抛物线对应的函数解析式；
（2）将图甲中△ABO沿x轴向左平移到△DCE（如图乙），当四边形ABCD是菱形时，请说明点C和点D都在该抛物线上；
（3）在（2）中，若点M是抛物线上的一个动点（点M不与点C、D重合），经过点M作MN∥y轴交直线CD于N，设点M的横坐标为t，MN的长度为l，求l与t之间的函数解析式，并求当t为何值时，以M、N、C、E为顶点的四边形是平行四边形．（参考公式：抛物线y=ax2+bx+c（a≠0）的顶点坐标为（﹣
， 
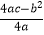），对称轴是直线x=﹣ ．） -
科目： 来源： 题型：
查看答案和解析>>【题目】先化简再求值
（1）3（x2﹣2x﹣1）﹣4（3x﹣2）+2（x﹣1）；其中x＝﹣3
（2）2a2﹣[
（ab﹣4a2）+8ab]﹣ab；其中a＝1，b＝
． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：在△ABC中，AC=a，AB与BC所在直线成45°角，AC与BC所在直线形成的夹角的余弦值为
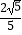（即cosC= 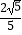），则AC边上的中线长是 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点A、B、C、D分别在正方形网格的格点上，其中A点的坐标为（﹣1，5），B点的坐标为（3，3），小明发现，线段AB与线段CD存在一种特殊关系，即其中一条线段绕着某点旋转一个角度可以得到另一条线段，则这个旋转中心的坐标是_____．
-
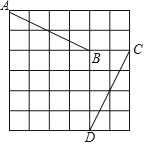
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，AD∥BC，AD=4，BC=12，点E是BC的中点．点P、Q分别是边AD、BC上的两点，其中点P以每秒个1单位长度的速度从点A运动到点D后再返回点A，同时点Q以每秒2个单位长度的速度从点C出发向点B运动．当其中一点到达终点时停止运动．当运动时间t为_____秒时，以点A、P，Q，E为顶点的四边形是平行四边形．
相关试题
