【题目】已知:在△ABC中,AC=a,AB与BC所在直线成45°角,AC与BC所在直线形成的夹角的余弦值为 ![]() (即cosC=
(即cosC= ![]() ),则AC边上的中线长是 .
),则AC边上的中线长是 .
参考答案:
【答案】![]() a或
a或 ![]() a
a
【解析】解:分两种情况: ①如图1.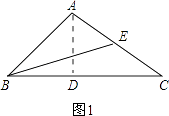
作△ABC的高AD,BE为AC边的中线.
∵在直角△ACD中,AC=a,cosC= ![]() ,
,
∴CD= ![]()
![]() a,AD=
a,AD= ![]() a.
a.
∵在直角△ABD中,∠ABD=45°,
∴BD=AD= ![]() a,
a,
∴BC=BD+CD= ![]() a.
a.
在△BCE中,由余弦定理,得
BE2=BC2+EC2﹣2BCECcosC
= ![]() a2+
a2+ ![]() a2﹣2×
a2﹣2× ![]() a×
a× ![]() a×
a× ![]()
= ![]() a2 ,
a2 ,
∴BE= ![]() a;
a;
②如图2.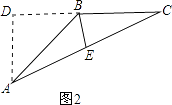
作△ABC的高AD,BE为AC边的中线.
∵在直角△ACD中,AC=a,cosC= ![]() ,
,
∴CD= ![]() a,AD=
a,AD= ![]() a.
a.
∵在直角△ABD中,∠ABD=45°,
∴BD=AD= ![]() a,
a,
∴BC=CD﹣BD= ![]() a.
a.
在△BCE中,由余弦定理,得
BE2=BC2+EC2﹣2BCECcosC
= ![]() a2+
a2+ ![]() a2﹣2×
a2﹣2× ![]() a×
a× ![]() a×
a× ![]()
= ![]() a2 ,
a2 ,
∴BE= ![]() a.
a.
综上可知AC边上的中线长是 ![]() a或
a或 ![]() a.
a.
所以答案是: ![]() a或
a或 ![]() a.
a.
【考点精析】本题主要考查了解直角三角形的相关知识点,需要掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲,在平面直角坐标系中,A、B的坐标分别为(4,0)、(0,3),抛物线y=
 x2+bx+c经过点B,且对称轴是直线x=﹣
x2+bx+c经过点B,且对称轴是直线x=﹣  .
.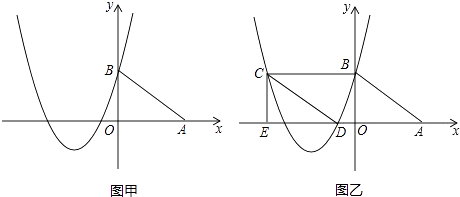
(1)求抛物线对应的函数解析式;
(2)将图甲中△ABO沿x轴向左平移到△DCE(如图乙),当四边形ABCD是菱形时,请说明点C和点D都在该抛物线上;
(3)在(2)中,若点M是抛物线上的一个动点(点M不与点C、D重合),经过点M作MN∥y轴交直线CD于N,设点M的横坐标为t,MN的长度为l,求l与t之间的函数解析式,并求当t为何值时,以M、N、C、E为顶点的四边形是平行四边形.(参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标为(﹣ ,
, 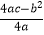 ),对称轴是直线x=﹣
),对称轴是直线x=﹣  .)
.) -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简再求值
(1)3(x2﹣2x﹣1)﹣4(3x﹣2)+2(x﹣1);其中x=﹣3
(2)2a2﹣[
 (ab﹣4a2)+8ab]﹣
(ab﹣4a2)+8ab]﹣ ab;其中a=1,b=
ab;其中a=1,b= .
. -
科目: 来源: 题型:
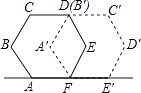
查看答案和解析>>【题目】如图,小红做了一个实验,将正六边形ABCDEF绕点F顺时针旋转后到达A′B′C′D′E′F′的位置,所转过的度数是( )
A.60°
B.72°
C.108°
D.120° -
科目: 来源: 题型:
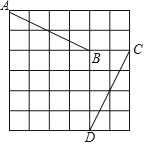
查看答案和解析>>【题目】如图,点A、B、C、D分别在正方形网格的格点上,其中A点的坐标为(﹣1,5),B点的坐标为(3,3),小明发现,线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,则这个旋转中心的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,AD=4,BC=12,点E是BC的中点.点P、Q分别是边AD、BC上的两点,其中点P以每秒个1单位长度的速度从点A运动到点D后再返回点A,同时点Q以每秒2个单位长度的速度从点C出发向点B运动.当其中一点到达终点时停止运动.当运动时间t为_____秒时,以点A、P,Q,E为顶点的四边形是平行四边形.

-
科目: 来源: 题型:
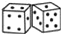
查看答案和解析>>【题目】骰子是一种特别的数字立方体(如图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( ).
A.
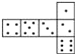 B.
B. 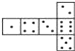 C.
C.  D.
D. 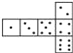
相关试题

