【题目】如图甲,在平面直角坐标系中,A、B的坐标分别为(4,0)、(0,3),抛物线y= ![]() x2+bx+c经过点B,且对称轴是直线x=﹣
x2+bx+c经过点B,且对称轴是直线x=﹣ ![]() .
.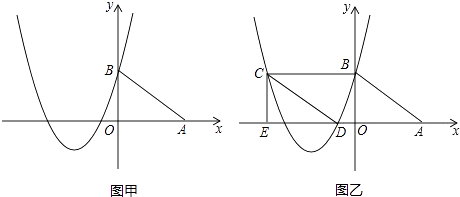
(1)求抛物线对应的函数解析式;
(2)将图甲中△ABO沿x轴向左平移到△DCE(如图乙),当四边形ABCD是菱形时,请说明点C和点D都在该抛物线上;
(3)在(2)中,若点M是抛物线上的一个动点(点M不与点C、D重合),经过点M作MN∥y轴交直线CD于N,设点M的横坐标为t,MN的长度为l,求l与t之间的函数解析式,并求当t为何值时,以M、N、C、E为顶点的四边形是平行四边形.(参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标为(﹣ ![]() ,
, ![]() ),对称轴是直线x=﹣
),对称轴是直线x=﹣ ![]() .)
.)
参考答案:
【答案】
(1)
解:由于抛物线y= ![]() x2+bx+c与y轴交于点B(0,3),则 c=3;
x2+bx+c与y轴交于点B(0,3),则 c=3;
∵抛物线的对称轴 x=﹣ ![]() =﹣
=﹣ ![]() ,
,
∴b=5a= ![]() ;
;
即抛物线的解析式:y= ![]() x2+
x2+ ![]() x+3.
x+3.
(2)
解:∵A(4,0)、B(0,3),
∴OA=4,OB=3,AB= ![]() =5;
=5;
若四边形ABCD是菱形,则BC=AD=AB=5,
∴C(﹣5,3)、D(﹣1,0).
将C(﹣5,3)代入y= ![]() x2+
x2+ ![]() x+3中,得:
x+3中,得: ![]() ×(﹣5)2+
×(﹣5)2+ ![]() ×(﹣5)+3=3,所以点C在抛物线上;
×(﹣5)+3=3,所以点C在抛物线上;
同理可证:点D也在抛物线上.
(3)
解:设直线CD的解析式为:y=kx+b,依题意,有:
![]() ,解得
,解得 
∴直线CD:y=﹣ ![]() x﹣
x﹣ ![]() .
.
由于MN∥y轴,设 M(t, ![]() t2+
t2+ ![]() t+3),则 N(t,﹣
t+3),则 N(t,﹣ ![]() t﹣
t﹣ ![]() );
);
② t<﹣5或t>﹣1时,l=MN=( ![]() t2+
t2+ ![]() t+3)﹣(﹣
t+3)﹣(﹣ ![]() t﹣
t﹣ ![]() )=
)= ![]() t2+
t2+ ![]() t+
t+ ![]() ;
;
②﹣5<t<﹣1时,l=MN=(﹣ ![]() t﹣
t﹣ ![]() )﹣(
)﹣( ![]() t2+
t2+ ![]() t+3)=﹣
t+3)=﹣ ![]() t2﹣
t2﹣ ![]() t﹣
t﹣ ![]() ;
;
若以M、N、C、E为顶点的四边形是平行四边形,由于MN∥CE,则MN=CE=3,则有:
![]() t2+
t2+ ![]() t+
t+ ![]() =3,解得:t1=﹣3+2
=3,解得:t1=﹣3+2 ![]() ,t2=﹣3﹣2
,t2=﹣3﹣2 ![]() ;
;
﹣ ![]() t2﹣
t2﹣ ![]() t﹣
t﹣ ![]() =3,解得:t=﹣3;
=3,解得:t=﹣3;
综上,l= 
且当t=﹣3+2 ![]() ,t=﹣3﹣2
,t=﹣3﹣2 ![]() 或﹣3时,以M、N、C、E为顶点的四边形是平行四边形.
或﹣3时,以M、N、C、E为顶点的四边形是平行四边形.
【解析】(1)抛物线y=ax2+bx+c中,(0,c)代表的是抛物线与y轴的交点,x=﹣ ![]() 是抛物线的对称轴,据此确定待定系数.(2)已知A、B点的坐标,由勾股定理能求出AB的长,若四边形ABCD是菱形,那么AD=BC=AB,可据此求出C、D点的坐标,再代入抛物线的解析式中进行验证即可.(3)在求l与t之间的函数解析式时,要分两种情况:①抛物线在直线CD上方、②抛物线在直线CD下方;先根据直线CD与抛物线的解析式,表示出M、N的坐标,它们纵坐标的差即为l的长,当以M、N、C、E为顶点的四边形是平行四边形时,由于CE∥MN∥y轴,那么CE必与MN相等,将CE长代入l、t的函数关系式中,即可求出符合条件的t的值.
是抛物线的对称轴,据此确定待定系数.(2)已知A、B点的坐标,由勾股定理能求出AB的长,若四边形ABCD是菱形,那么AD=BC=AB,可据此求出C、D点的坐标,再代入抛物线的解析式中进行验证即可.(3)在求l与t之间的函数解析式时,要分两种情况:①抛物线在直线CD上方、②抛物线在直线CD下方;先根据直线CD与抛物线的解析式,表示出M、N的坐标,它们纵坐标的差即为l的长,当以M、N、C、E为顶点的四边形是平行四边形时,由于CE∥MN∥y轴,那么CE必与MN相等,将CE长代入l、t的函数关系式中,即可求出符合条件的t的值.
【考点精析】解答此题的关键在于理解菱形的性质的相关知识,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】6月5日是世界环境日,某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级的一班和二班的成绩整理并绘制成统计图: 根据以上提供的信息解答下列问题:

(1)把一班竞赛成绩统计图补充完整;
(2)写出下表中a、b、c的值:平均数(分)
中位数(分)
众数(分)
一班
a
b
90
二班
87.6
80
c
(3)请从以下给出的三个方面中任选一个对这次竞赛成绩的结果进行分析: ①从平均数和中位数方面比较一班和二班的成绩;②从平均数和众数方面比较一班和二班的成绩;③从B级以上(包括B级)的人数方面来比较一班和二班的成绩. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,小明在自家楼顶上的点A处测量建在与小明家楼房同一水平线上邻居的电梯的高度,测得电梯楼顶部B处的仰角为45°,底部C处的俯角为26°,已知小明家楼房的高度AD=15米,求电梯楼的高度BC(结果精确到0.1米)(参考数据:sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)
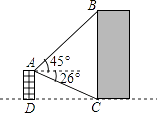
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.

(1)求证:EF是⊙O的切线;
(2)求证:AC2=ADAB;
(3)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简再求值
(1)3(x2﹣2x﹣1)﹣4(3x﹣2)+2(x﹣1);其中x=﹣3
(2)2a2﹣[
 (ab﹣4a2)+8ab]﹣
(ab﹣4a2)+8ab]﹣ ab;其中a=1,b=
ab;其中a=1,b= .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小红做了一个实验,将正六边形ABCDEF绕点F顺时针旋转后到达A′B′C′D′E′F′的位置,所转过的度数是( )
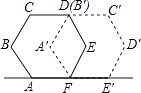
A.60°
B.72°
C.108°
D.120° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在△ABC中,AC=a,AB与BC所在直线成45°角,AC与BC所在直线形成的夹角的余弦值为
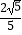 (即cosC=
(即cosC= 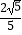 ),则AC边上的中线长是 .
),则AC边上的中线长是 .
相关试题

