【题目】出租车司机小李某天上午营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接六位乘客的行车里程(单位:![]() )如下:
)如下:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
问:(1)将最后一位乘客送到目的地时,小李在什么位置?
(2)若汽车耗油量为![]() (升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(3)若出租车起步价为8元,起步里程为![]() (包括
(包括![]() ),超过部分每千米1.2元,问小李这天上午共得车费多少元?
),超过部分每千米1.2元,问小李这天上午共得车费多少元?
参考答案:
【答案】(1)在起始的西的位置5km处;(2)3.4L;(3)54元
【解析】
(1)先将这几个数相加,若和为正,则在出发点的东方;若和为负,则在出发点的西方;
(2)将这几个数的绝对值相加,再乘以耗油量,即可得出答案;
(3)不超过3km的按8元计算,超过3km的在8元的基础上,再加上超过部分乘以1.2元,即可求解.
(1)![]()
所以小李在起始的西的位置![]()
(2)![]()
![]() (升)
(升)
答:出租车共耗油3.4升.
(3)![]() (元)
(元)
答:小李这天上午共得车费54元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习过程中,对教材中的一个有趣问题做如下探究:

(习题回顾)已知:如图1,在
 中,
中, ,
, 是角平分线,
是角平分线, 是高,
是高, 、
、 相交于点
相交于点 .求证:
.求证: ;
;(变式思考)如图2,在
 中,
中, ,
, 是
是 边上的高,若
边上的高,若 的外角
的外角 的平分线交
的平分线交 的延长线于点
的延长线于点 ,其反向延长线与
,其反向延长线与 边的延长线交于点
边的延长线交于点 ,则
,则 与
与 还相等吗?说明理由;
还相等吗?说明理由;(探究延伸)如图3,在
 中,
中, 上存在一点
上存在一点 ,使得
,使得 ,
, 的平分线
的平分线 交
交 于点
于点 .
. 的外角
的外角 的平分线所在直线
的平分线所在直线 与
与 的延长线交于点
的延长线交于点 .直接写出
.直接写出 与
与 的数量关系.
的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高.某社区为了了解家庭对于文化教育的消费情况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调查,根据调查结果绘制成如下两幅不完整的统计图表.
组別
家庭年文化教育消费金额x(元)
户数
A
x≤5000
36
B
5000<x≤10000
27
C
10000<x≤15000
m
D
15000<x≤20000
33
E
x>20000
30
请你根据统计图表提供的信息,解答下列问题:
(1)本次被调查的家庭有 户,表中m= ;
(2)请说明本次调查数据的中位数落在哪一组?
(3)在扇形统计图中,D组所在扇形的圆心角为多少度?
(4)这个社区有2500户家庭,请你估计年文化教育消费在10000元以上的家庭有多少户?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,AB∥CD,∠BCF=180°,BD平分∠ABC,CE平分∠DCF,∠ACE=90°.
求证:AC⊥BD

请将下列证明过程中的空格补充完整.
证明:∵AB∥CD,
∴∠ABC=∠DCF.(_____)
∵BD平分∠ABC,CE平分∠DCF,
∴∠2=
 ∠ABC,∠4=
∠ABC,∠4= ∠DCF.(_____)
∠DCF.(_____)∴_______.
∴BD∥CE.(_______)
∴______.(两直线平行,内错角相等)
∵∠ACE=90°,
∴∠BGC=90°,即AC⊥BD.(_____)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
 的图象在第二、四象限,一次函数为y=kx+b(b>0),直线x=1与x轴交于点B,与直线y=kx+b交于点A,直线x=3与x轴交于点C,与直线y=kx+b交于点D.点A,D都在第一象限,直线y=kx+b与x轴交于点E,与y轴交于点F
的图象在第二、四象限,一次函数为y=kx+b(b>0),直线x=1与x轴交于点B,与直线y=kx+b交于点A,直线x=3与x轴交于点C,与直线y=kx+b交于点D.点A,D都在第一象限,直线y=kx+b与x轴交于点E,与y轴交于点F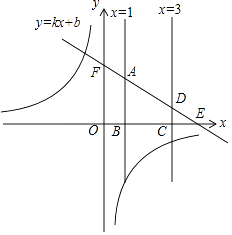
(1)当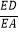 =
=  且△OFE的面积等于
且△OFE的面积等于 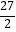 时,求这个一次函数的解析式;
时,求这个一次函数的解析式;
(2)在(1)的条件下,根据函数图象,试求不等式 >kx+b的解集.
>kx+b的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形OABC的边长为4,对角线相交于点P,顶点A,C分别在x轴,y轴的正半轴上,抛物线L经过O,P,A三点,点E是正方形内的抛物线上的动点.
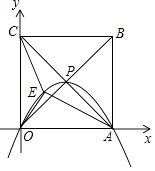
(1)点P的坐标为;
(2)求抛物线L的解析式;
(3)求△OAE与△OCE面积之和的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】【探究证明】某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
如图1,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H.求证: =
= 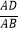 ;
;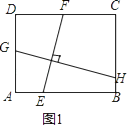
(2)【结论应用】如图2,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若 =
= 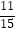 ,则
,则 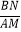 的值为;
的值为;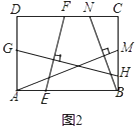
(3)【联系拓展】如图3,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求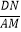 的值.
的值.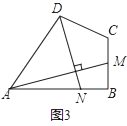
相关试题

