【题目】小明在学习过程中,对教材中的一个有趣问题做如下探究:

(习题回顾)已知:如图1,在![]() 中,
中,![]() ,
,![]() 是角平分线,
是角平分线,![]() 是高,
是高,![]() 、
、![]() 相交于点
相交于点![]() .求证:
.求证:![]() ;
;
(变式思考)如图2,在![]() 中,
中,![]() ,
,![]() 是
是![]() 边上的高,若
边上的高,若![]() 的外角
的外角![]() 的平分线交
的平分线交![]() 的延长线于点
的延长线于点![]() ,其反向延长线与
,其反向延长线与![]() 边的延长线交于点
边的延长线交于点![]() ,则
,则![]() 与
与![]() 还相等吗?说明理由;
还相等吗?说明理由;
(探究延伸)如图3,在![]() 中,
中,![]() 上存在一点
上存在一点![]() ,使得
,使得![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() .
.![]() 的外角
的外角![]() 的平分线所在直线
的平分线所在直线![]() 与
与![]() 的延长线交于点
的延长线交于点![]() .直接写出
.直接写出![]() 与
与![]() 的数量关系.
的数量关系.
参考答案:
【答案】[习题回顾]证明见解析;[变式思考] 相等,证明见解析;[探究延伸] ∠M+∠CFE=90°,证明见解析.
【解析】
[习题回顾]根据同角的余角相等可证明∠B=∠ACD,再根据三角形的外角的性质即可证明;
[变式思考]根据角平分线的定义和对顶角相等可得∠CAE=∠DAF、再根据直角三角形的性质和等角的余角相等即可得出![]() =
=![]() ;
;
[探究延伸]根据角平分线的定义可得∠EAN=90°,根据直角三角形两锐角互余可得∠M+∠CEF=90°,再根据三角形外角的性质可得∠CEF=∠CFE,由此可证∠M+∠CFE=90°.
[习题回顾]证明:∵∠ACB=90°,CD是高,
∴∠B+∠CAB=90°,∠ACD+∠CAB=90°,
∴∠B=∠ACD,
∵AE是角平分线,
∴∠CAF=∠DAF,
∵∠CFE=∠CAF+∠ACD,∠CEF=∠DAF+∠B,
∴∠CEF=∠CFE;
[变式思考]相等,理由如下:
证明:∵AF为∠BAG的角平分线,
∴∠GAF=∠DAF,
∵∠CAE=∠GAF,
∴∠CAE=∠DAF,
∵CD为AB边上的高,∠ACB=90°,
∴∠ADC=90°,
∴∠ADF=∠ACE=90°,
∴∠DAF+∠F=90°,∠E+∠CAE=90°,
∴∠CEF=∠CFE;
[探究延伸]∠M+∠CFE=90°,
证明:∵C、A、G三点共线AE、AN为角平分线,
∴∠EAN=90°,
又∵∠GAN=∠CAM,
∴∠M+∠CEF=90°,
∵∠CEF=∠EAB+∠B,∠CFE=∠EAC+∠ACD,∠ACD=∠B,
∴∠CEF=∠CFE,
∴∠M+∠CFE=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图为放置在水平桌面上的台灯的平面示意图,可伸缩式灯臂AO长为40cm,与水平面所形成的夹角∠OAM恒为75°(不受灯臂伸缩的影响),由光源O射出的光线沿灯罩形成光线OC,OB与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°,

(1)求该台灯照亮桌面的宽度BC(不考虑其他因素,结果精确到1cm.温馨提示:sin75°≈0.97,cos75°≈0.26,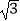 ≈1.73)
≈1.73)
(2)若灯臂最长可伸长至60cm,不调整灯罩的角度,能否让台灯照亮桌面85cm的宽度? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ACDF中,AC=DF,点B在CD上,点E在DF上,BC=DE=a,AC=BD=b,AB=BE=c,且AB⊥BE.

(1)用两种不同的方法表示长方形ACDF的面积S
方法一:S=
方法二:S=
(2)求a,b,c之间的等量关系(需要化简)
(3)请直接运用(2)中的结论,求当c=5,a=3,S的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A1,A2,A3,…分别在x轴上,点B1,B2,B3,…分别在直线y=x上,△OA1B1,△B1A1A2,△B1B2A2,△B2A2A3,△B2B3A3…,都是等腰直角三角形,如果OA1=1,则点A2019的坐标为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高.某社区为了了解家庭对于文化教育的消费情况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调查,根据调查结果绘制成如下两幅不完整的统计图表.
组別
家庭年文化教育消费金额x(元)
户数
A
x≤5000
36
B
5000<x≤10000
27
C
10000<x≤15000
m
D
15000<x≤20000
33
E
x>20000
30
请你根据统计图表提供的信息,解答下列问题:
(1)本次被调查的家庭有 户,表中m= ;
(2)请说明本次调查数据的中位数落在哪一组?
(3)在扇形统计图中,D组所在扇形的圆心角为多少度?
(4)这个社区有2500户家庭,请你估计年文化教育消费在10000元以上的家庭有多少户?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,AB∥CD,∠BCF=180°,BD平分∠ABC,CE平分∠DCF,∠ACE=90°.
求证:AC⊥BD

请将下列证明过程中的空格补充完整.
证明:∵AB∥CD,
∴∠ABC=∠DCF.(_____)
∵BD平分∠ABC,CE平分∠DCF,
∴∠2=
 ∠ABC,∠4=
∠ABC,∠4= ∠DCF.(_____)
∠DCF.(_____)∴_______.
∴BD∥CE.(_______)
∴______.(两直线平行,内错角相等)
∵∠ACE=90°,
∴∠BGC=90°,即AC⊥BD.(_____)
-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机小李某天上午营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接六位乘客的行车里程(单位:
 )如下:
)如下: ,
, ,
, ,
, ,
, ,
, ,
,问:(1)将最后一位乘客送到目的地时,小李在什么位置?
(2)若汽车耗油量为
 (升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(升/千米),这天上午小李接送乘客,出租车共耗油多少升?(3)若出租车起步价为8元,起步里程为
 (包括
(包括 ),超过部分每千米1.2元,问小李这天上午共得车费多少元?
),超过部分每千米1.2元,问小李这天上午共得车费多少元?
相关试题

