【题目】如图,抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,图象与
,图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点.
两点.

![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 设抛物线对称轴与直线
设抛物线对称轴与直线![]() 交于点
交于点![]() ,连接
,连接![]() 、
、![]() ,求
,求![]() 的面积;
的面积;
![]() 点
点![]() 为直线
为直线![]() 上的任意一点,过点
上的任意一点,过点![]() 作
作![]() 轴的垂线与抛物线交于点
轴的垂线与抛物线交于点![]() ,问是否存在点
,问是否存在点![]() 使
使![]() 为直角三角形?若存在,求出点
为直角三角形?若存在,求出点![]() 坐标,若不存在,请说明理由.
坐标,若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)2;(3)见解析.
;(2)2;(3)见解析.
【解析】
(1)可设抛物线解析式为顶点式,把C点坐标代入可求得抛物线解析式;
(2)由抛物线解析式可求得A、B坐标,利用待定系数法可求得直线BC解析式,利用对称轴可求得D点坐标,则可求得AD2、AC2和CD2,利用勾股定理的逆定理可判定△ACD为直角三角形,则可求得其面积;
(3)根据题意可分∠DFE=90°和∠EDF=90°两种情况,当∠DFE=90°时,可知DF∥x轴,则可求得E点纵坐标,代入抛物线解析式可求得E点坐标;当∠EDF=90°时,可求得直线AD解析式,联立直线AC和抛物线解析式可求得点E的横坐标,代入直线BC可求得点E的坐标.
解:![]() ∵抛物线的顶点坐标为
∵抛物线的顶点坐标为![]() ,
,
∴可设抛物线解析式为![]() ,
,
把![]() 代入可得
代入可得![]() ,解得
,解得![]() ,
,
∴抛物线解析式为![]() ;
;
![]() 在
在![]() 中,令
中,令![]() 可得
可得![]() ,解得
,解得![]() 或
或![]() ,
,
∴![]() ,
,![]() ,
,
设直线![]() 解析式为
解析式为![]() ,把
,把![]() 代入得:
代入得:![]() ,解得
,解得![]() ,
,
∴直线![]() 解析式为
解析式为![]() ,
,
由![]() 可知抛物线的对称轴为
可知抛物线的对称轴为![]() ,此时
,此时![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() 是以
是以![]() 为斜边的直角三角形,
为斜边的直角三角形,
∴![]() ;
;
![]() 由题意知
由题意知![]() 轴,则
轴,则![]() ,
,
∴![]() 为直角三角形,分
为直角三角形,分![]() 和
和![]() 两种情况,
两种情况,
①当![]() 时,即
时,即![]() 轴,则
轴,则![]() 、
、![]() 的纵坐标相同,
的纵坐标相同,
∴![]() 点纵坐标为
点纵坐标为![]() ,
,
∵点![]() 在抛物线上,
在抛物线上,
∴![]() ,解得
,解得![]() ,即点
,即点![]() 的横坐标为
的横坐标为![]() ,
,
∵点![]() 在直线
在直线![]() 上,
上,
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 点坐标为
点坐标为![]() 或
或![]() ;
;
②当![]() 时,
时,
∵![]() ,
,![]() ,
,
∴直线![]() 解析式为
解析式为![]() ,
,
∵直线![]() 解析式为
解析式为![]() ,
,
∴![]() ,
,
∴直线![]() 与抛物线的交点即为
与抛物线的交点即为![]() 点,
点,
联立直线![]() 与抛物线解析式有
与抛物线解析式有![]() ,解得
,解得![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 点坐标为
点坐标为![]() 或
或![]() ,
,
综上可知存在满足条件的点![]() ,其坐标为
,其坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 是关于
是关于 的二次函数.求:
的二次函数.求: 满足条件的
满足条件的 的值;
的值; 为何值时,抛物线有最低点?求出这个最低点,这时当
为何值时,抛物线有最低点?求出这个最低点,这时当 为何值时,
为何值时, 随
随 的增大而增大?
的增大而增大? 为何值时,函数有最大值?最大值是多少?这时当
为何值时,函数有最大值?最大值是多少?这时当 为何值时,
为何值时, 随
随 的增大而减小?
的增大而减小? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点
 ,以
,以 为直径在第一象限内作半圆,
为直径在第一象限内作半圆, 为半圆上一点,连接
为半圆上一点,连接 并延长至
并延长至 ,使
,使 ,过
,过 作
作 轴于点
轴于点 ,交线段
,交线段 于点
于点 ,已知
,已知 ,抛物线经过
,抛物线经过 、
、 、
、 三点.
三点.
 ________°.
________°. 求抛物线的函数表达式.
求抛物线的函数表达式. 若
若 为抛物线上位于第一象限内的一个动点,以
为抛物线上位于第一象限内的一个动点,以 、
、 、
、 、
、 为顶点的四边形面积记作
为顶点的四边形面积记作 ,则
,则 取何值时,相应的点
取何值时,相应的点 有且只有
有且只有 个?
个? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一个长为
 米的篱笆,一面利用墙(墙的最大长度
米的篱笆,一面利用墙(墙的最大长度 为
为 米)围成的中间隔有一道篱笆的长方形花圃.设花圃的宽
米)围成的中间隔有一道篱笆的长方形花圃.设花圃的宽 为
为 米,面积为
米,面积为 平方米.
平方米.
 求
求 与
与 的函数关系式;
的函数关系式; 如果要围成花圃的面积为
如果要围成花圃的面积为 平方米,求
平方米,求 的长为多少米?
的长为多少米? 如果要使围成花圃面积最大,求
如果要使围成花圃面积最大,求 的长为多少米?
的长为多少米? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平行四边形ABCD中,BC=3,AB=4,
 ,E为线段BC上任意一点,连接AE并延长与DC交于点G,若BE=2EC,则AE的边长为( )
,E为线段BC上任意一点,连接AE并延长与DC交于点G,若BE=2EC,则AE的边长为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、点B是双曲线
 图象上的两点(A在B的右侧).延长AB交y轴正半轴于C,OC的中点为D.连结AO,BO,交点为E.若△BEO的面积为4,四边形AEDC的面积等于△BEO的面积,则k的值为_______.
图象上的两点(A在B的右侧).延长AB交y轴正半轴于C,OC的中点为D.连结AO,BO,交点为E.若△BEO的面积为4,四边形AEDC的面积等于△BEO的面积,则k的值为_______.
-
科目: 来源: 题型:
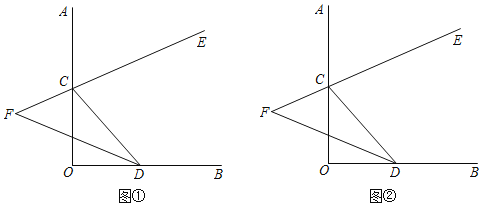
查看答案和解析>>【题目】如图,∠AOB=90°,点C,D分别在射线OA,OB上,CE是∠ACD的平分线,CE的反向延长线与∠CDO的平分线交于点F.
(1)当∠OCD=56°(如图①),试求∠F;
(2)当C,D在射线OA、OB上任意移动时(不与点O重合)(如图②),∠F的大小是否变化?若变化,请说明理由若不变化求出∠F.
相关试题

