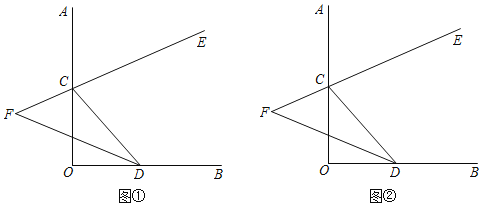
【题目】如图,∠AOB=90°,点C,D分别在射线OA,OB上,CE是∠ACD的平分线,CE的反向延长线与∠CDO的平分线交于点F.
(1)当∠OCD=56°(如图①),试求∠F;
(2)当C,D在射线OA、OB上任意移动时(不与点O重合)(如图②),∠F的大小是否变化?若变化,请说明理由若不变化求出∠F.
参考答案:
【答案】(1)∠F=45°;(2)不变,∠F=45°.
【解析】
(1)首先求出∠CDO=34°,∠ACD=124°,进而得到∠ECD=62°,∠CDF=17°,再根据三角形的外角等于与它不相邻的两内角之和,可求∠F=∠ECD﹣∠CDF;
(2)根据三角形外角的性质和角平分线定义求出∠ECD=![]() (90°+∠CDO),∠CDF=
(90°+∠CDO),∠CDF=![]() ∠CDO,然后根据三角形的外角等于与它不相邻的两内角之和,可求∠F=∠ECD﹣∠CDF.
∠CDO,然后根据三角形的外角等于与它不相邻的两内角之和,可求∠F=∠ECD﹣∠CDF.
(1)∵∠AOB=90°,∠OCD=56°,
∴∠CDO=34°,∠ACD=124°,
∵CE是∠ACD的平分线,DF是∠CDO的平分线,
∴∠ECD=62°,∠CDF=17°,
∵∠ECD=∠F+∠CDF,
∴∠F=∠ECD -∠CDF =45°;
(2)∠F不变,
∵∠ECD=![]() ∠ACD=
∠ACD=![]() (90°+∠CDO),
(90°+∠CDO),
∴∠ECD=45°+![]() ∠CDO,
∠CDO,
∵∠CDF=![]() ∠CDO,
∠CDO,
∴∠F=∠ECD﹣∠CDF,
=45°+![]() ∠CDO﹣
∠CDO﹣![]() ∠CDO,
∠CDO,
=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 的顶点坐标为
的顶点坐标为 ,图象与
,图象与 轴交于点
轴交于点 ,与
,与 轴交于
轴交于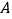 、
、 两点.
两点.
 求抛物线的解析式;
求抛物线的解析式; 设抛物线对称轴与直线
设抛物线对称轴与直线 交于点
交于点 ,连接
,连接 、
、 ,求
,求 的面积;
的面积; 点
点 为直线
为直线 上的任意一点,过点
上的任意一点,过点 作
作 轴的垂线与抛物线交于点
轴的垂线与抛物线交于点 ,问是否存在点
,问是否存在点 使
使 为直角三角形?若存在,求出点
为直角三角形?若存在,求出点 坐标,若不存在,请说明理由.
坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平行四边形ABCD中,BC=3,AB=4,
 ,E为线段BC上任意一点,连接AE并延长与DC交于点G,若BE=2EC,则AE的边长为( )
,E为线段BC上任意一点,连接AE并延长与DC交于点G,若BE=2EC,则AE的边长为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、点B是双曲线
 图象上的两点(A在B的右侧).延长AB交y轴正半轴于C,OC的中点为D.连结AO,BO,交点为E.若△BEO的面积为4,四边形AEDC的面积等于△BEO的面积,则k的值为_______.
图象上的两点(A在B的右侧).延长AB交y轴正半轴于C,OC的中点为D.连结AO,BO,交点为E.若△BEO的面积为4,四边形AEDC的面积等于△BEO的面积,则k的值为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠EDC= °,∠DEC= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】王老师给学生出了一道题:求(2a+b)(2a﹣b)+2(2a﹣b)2+(2ab2﹣16a2b)÷(﹣2a)的值,其中a=
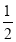 ,b=﹣1,同学们看了题目后发表不同的看法.小张说:条件b=﹣1是多余的.”小李说:“不给这个条件,就不能求出结果,所以不多余.”你认为他们谁说的有道理?为什么?
,b=﹣1,同学们看了题目后发表不同的看法.小张说:条件b=﹣1是多余的.”小李说:“不给这个条件,就不能求出结果,所以不多余.”你认为他们谁说的有道理?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD//BC,
 ,
, ,
, ,
, ,动点M从B点出发沿线段BC以每秒2个单位长度的速度向C运动;动点N同时从A点出发沿线段AB以每秒1个单位长度的速度向B运动,其中一点到达终点时,则两点同时停止运动.设运动的时间为t秒,当△MNB为等腰直角三角形时,t的值是_______.
,动点M从B点出发沿线段BC以每秒2个单位长度的速度向C运动;动点N同时从A点出发沿线段AB以每秒1个单位长度的速度向B运动,其中一点到达终点时,则两点同时停止运动.设运动的时间为t秒,当△MNB为等腰直角三角形时,t的值是_______.
相关试题

