Question

【题目】如图1，在平面直角坐标系中，A（a，0），B（0，2）

（1）点（k+1，2k﹣5）关于x轴的对称点在第一象限，a为实数k的范围内的最大整数，求A点的坐标及△AOB的面积；

（2）在（1）的条件下如图1，点P是第一象限内的点，且△ABP是以AB为腰的等腰直角三角形，请直接写出P点坐标；

（3）在（1）的条件下，如图2，以AB、OB的作等边△ABC和等边△OBD，连接AD、OC交于E点，连接BE．

①求证：EB平分∠CED；

②M点是y轴上一动点，求AM+CM最小时点M的坐标．

Answer 1

【答案】（1）A（2，0），S△AOB＝2；（2）P点坐标为（2+2，2）或（2，2+2）；（3）①详见解析；②M（0，）．

【解析】

（1）根据点在第四象限内，得出不等式，进而求出k的范围，进而求出点A坐标，最后用三角形面积公式即可得出结论；

（2）分两种情况：构造全等三角形求出PF和AF，即可求出点P坐标；

（3）①先判断出△ABD≌△CBO（SAS），进而得出S△ABD＝S△CBO，AD＝OC，即可得出BM＝BN，最后用角平分线的判定定理即可得出结论；

②根据含30度角的直角三角形的性质求出线段的长，进而求出点C坐标，求出直线A'C的解析式，即可得出结论．

解：（1）∵点（k+1，2k﹣5）关于x轴的对称点在第一象限，

∴点（k+1，2k﹣5）在第四象限，

∴k+1＞0，2k﹣5＜0，

∴﹣1＜k＜2.5，

∵a为实数k的范围内的最大整数，

∴a＝2，

∵A（a，0），

∴A（2，0），

∴OA＝2，

∵B（0，2），

∴OB＝2，

∴S△AOB＝OAOB＝×＝2；

（2）如图1，

∵点P是第一象限内的点，且△ABP是以AB为腰的等腰直角三角形，

∴①当∠BAP＝90°时，AB＝AP，

过点P作PF⊥OA于F，

∴∠PAF+∠APF＝90°，

∵∠BAP＝90°，

∴∠PAF+∠BAO＝90°，

∴∠APF＝∠BAO，

∵AB＝AP，

∴△OAB≌△FPA（AAS），

∴PF＝OA＝2，AF＝OB＝2，

∴OF＝OA+AF＝2+2，

∴P（+2，2），

②当∠ABP＝90°时，同①的方法得，P'（2，2+2），

即：P点坐标为（2+2，2）或（2，2+2）；

（3）①如图2，

∵△OBD和△ABC都是等边三角形，

∴BD＝OB，AB＝BC，∠OBD＝∠ABC＝60°，

∴∠ABD＝∠CBO，

在△ABD和△CBO中，，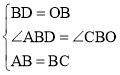

∴△ABD≌△CBO（SAS），

∴S△ABD＝S△CBO，AD＝OC，

过点B作BM⊥AD于M，BN⊥OC于N，

∴BM＝BN，

∵BM⊥AD，BN⊥OC，

∴BE是∠CED的角平分线；

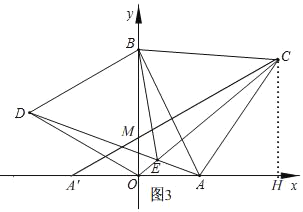
②如图3，

作点A关于y轴的对称点A'，

∵A（2，0），

∴A'（﹣2，0），

连接A'C交y轴于M，

过点C作CH⊥OA于H，

在Rt△AOB中，OA＝2，OB＝2，

∴AB＝4，tan∠OAB＝＝＝，

∴∠OAB＝60°，

∵△ABC是等边三角形，

∴AC＝AB＝4，∠BAC＝60°，

∴∠CAH＝60°，

在Rt△ACH中，∠ACH＝90°﹣∠CAH＝30°，

∴AH＝2，CH＝2，

∴OH＝OA+AH＝4，

∴点C（4，2），

∵A'（﹣2，0），

∴直线A'C的解析式为y＝x+，

∴M（0，）．