Question

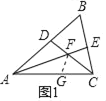
【题目】在△ABC中，∠B＝60°，D、E分别为AB、BC上的点，且AE、CD交于点F．

（1）如图1，若AE、CD为△ABC的角平分线：

①求∠AFD的度数；

②若AD＝3，CE＝2，求AC的长；

（2）如图2，若∠EAC＝∠DCA＝30°，求证：AD＝CE．

Answer 1

【答案】（1）①60°；②5；（2）详见解析.

【解析】

（1）①根据角平分线的定义、三角形内角和定理计算；

②在AC上截取AG＝AD＝3，连接FG，证明△ADF≌△AGF、△CGF≌△CEF，根据全等三角形的性质解答；

（2）在AE上截取FH＝FD，连接CH，证明△ADF≌△CHF，根据全等三角形的性质、三角形的外角的性质解答．

解：（1）①∵AE、CD分别为△ABC的角平分线，

∴∠FAC＝∠BAC，∠FCA＝∠BCA，

∵∠B＝60°

∴∠BAC+∠BCA＝120°，

∴∠AFC＝180﹣∠FAC﹣∠FCA＝180﹣（∠BAC+∠BCA）＝120°

∴∠AFD=180°-∠AFC=60°；

②在AC上截取AG＝AD＝3，连接FG，

∵AE、CD分别为△ABC的角平分线，

∴∠FAC＝∠FAD，∠FCA＝∠FCE，

∵∠AFC＝120°，

∴∠AFD＝∠CFE＝60°，

在△ADF和△AGF中，

∵，

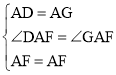∴△ADF≌△AGF（SAS），

∴∠AFD＝∠AFG＝60°，

∴∠GFC＝∠CFE＝60°，

在△CGF和△CEF中，

∵，

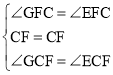∴△CGF≌△CEF（ASA），

∴CG＝CE＝2，

∴AC＝5；

（2）在AE上截取FH＝FD，连接CH，

∵∠FAC＝∠FCA＝30°，

∴FA＝FC，

在△ADF和△CHF中，

∵，

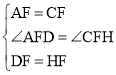∴△ADF≌△CHF（SAS），

∴AD＝CH，∠DAF＝∠HCF，

∵∠CEH＝∠B+∠DAF＝60°+∠DAF，

∠CHE＝∠HAC+∠HCA＝60°+∠HCF，

∴∠CEH＝∠CHE，

∴CH＝CE，

∴AD＝CE．