Question

【题目】如图（1），四边形ABCD是平行四边形，BD是它的一条对角线，过顶点A、C分别作AM⊥BD，CN⊥BD，M，N为垂足．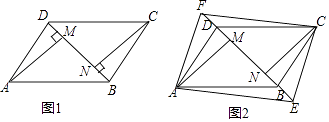
（1）求证：AM=CN；
（2）如图（2），在对角线DB的延长线及反向延长线上分别取点E，F，使BE=DF，连接AE、CF，试探究：当EF满足什么条件时，四边形AECF是矩形？并加以证明．

Answer 1

【答案】
（1）证明：∵四边形ABCD是平行四边形，

∴AD=BC，AD∥BC，∠ADM=∠CBN．

∵AM⊥BD，CN⊥BD，

∴∠AMD=∠CNB=90°，

在△AMD和△CNB中 ，

∴△AMD≌△CNB．

∴AM=CN．

（2）猜想：当EF=AC时，四边形AECF是矩形．

证明：由（1）得△AMD≌△CNB，

∴DM=BN．

∵BE=DF，

∴DM+DF=BN+BE，即MF=NE．

在△AMF和△CNE中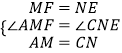

∴△AMF≌△CNE．

∴AF=CE，∠AFE=∠CEF．

∴AF∥CE且AF=CE．

即四边形AECF是平行四边形．

又EF=AC，

∴四边形AMCN是矩形

【解析】（1）利用平行四边形的性质证得△AMD≌△CNB，从而根据全等三角形对应边相等证得结论即可；（2）利用对角线相等的平行四边形是矩形证得结论即可．
【考点精析】通过灵活运用平行四边形的性质和矩形的判定方法，掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分；有一个角是直角的平行四边形叫做矩形；有三个角是直角的四边形是矩形；两条对角线相等的平行四边形是矩形即可以解答此题．