搜索
【题目】如图，直线
与x轴交于点
，直线
与x轴、y轴分别交于B、C两点，并与直线相交于点D，若
．
求点D的坐标；
求出四边形AOCD的面积；
若E为x轴上一点，且
为等腰三角形，写出点E的坐标
直接写出答案
．
参考答案：
【答案】（1）
点坐标为
；（2）
；（3）点E的坐标为
、
、
、
，
、
、
．
【解析】
先确定直线
的解析式，进而求出点
的坐标，再分两种情况：
Ⅰ、当点在点
右侧时，
（1）把点坐标代入
可得到
，则
，然后根据两直线相交的问题，通过解方程组
得到点坐标；
（2）先确定
点坐标为
然后利用四边形
的面积
进行计算即可；
（3）设出点
的坐标，进而表示出
，再利用等腰三角形的两腰相等建立方程，即可得出结论；
Ⅱ、当点在点左侧时，
同Ⅰ的方法即可得出结论.
解：把
代入
得
，解得
，
，
设
，
，，
，
或
，
点坐标为或
，
Ⅰ、当
时，
把代入
得
，解得，
，
解方程组
得
，
点坐标为；
当
时，
，
点坐标为
，
四边形AOCD的面积
；
设
，
，
，
，
，
，
是等腰三角形，
当
时，
，
或
，
或
当
时，
，
或
舍
，
当
时，
，
，
，
Ⅱ、当点
时，
把代入得
，解得
，
，
解方程组
，得
，
点坐标为
；
当时，
，
点坐标为
，
四边形AOCD的面积
；
设
，
，
，
，
当时，
，
或
，
或
当时，
，
或舍
，
当时，
，
，
，
综上所述，点E的坐标为、、、，、、．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，一次函数的图象经过点A（2，3）与点B（0，5）．
（1）求此一次函数的表达式；
（2）若点P为此一次函数图象上一点，且△POB的面积为10，求点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图（1），四边形ABCD是平行四边形，BD是它的一条对角线，过顶点A、C分别作AM⊥BD，CN⊥BD，M，N为垂足．
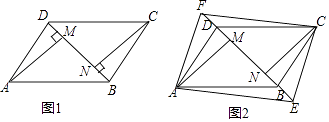
（1）求证：AM=CN；
（2）如图（2），在对角线DB的延长线及反向延长线上分别取点E，F，使BE=DF，连接AE、CF，试探究：当EF满足什么条件时，四边形AECF是矩形？并加以证明． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图AB∥CD．∠1=∠2，∠3=∠4，试说明AD∥BE．
解：∵AB∥CD（已知）
∴∠4=∠ （ ）
∵∠3=∠4（已知）
∴∠3=∠ （ ）
∵∠1=∠2（已知）
∴∠1+∠CAF=∠2+∠CAF（
即∠ =∠ （ ）
∴∠3=∠
∴AD∥BE（ ）
-
科目： 来源： 题型：
查看答案和解析>>【题目】某车间有技术工人85人，平均每天每人可加工甲种部件16个或乙种部件10个，2个甲种部件和3个乙种部件配成一套，问加工甲、乙两种部件各安排多少人才能使每天加工的两种部件刚好配套？并求出加工了多少套？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，△ABE≌△ADC≌△ABC，若∠1∶∠2∶∠3=28∶5∶3，则∠α的度数为（ ）
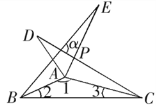
A. 80° B. 100° C. 60° D. 45°
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图（1），在平面直角坐标系中，抛物线y=﹣
x2+bx+c与x轴交于点A（﹣4，0），与y轴交于点B（0，4）．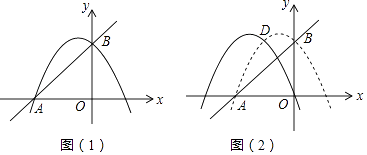
（1）求抛物线的函数解析式；
（2）在x轴上有一点P，点P在直线AB的垂线段为PC，C为垂足，且PC=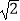
，求点P的坐标；
（3）如图（2），将原抛物线向左平移，使平移后的抛物线过原点，与原抛物线交于点D，在平移后的抛物线上是否存在点E，使S△APE=S△ACD？若存在，请求出点E的坐标，若不存在，请说明理由．
相关试题
