【题目】为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题.
组别 | 成绩x(分) | 频数(人数) |
A | 8.0≤x<8.5 | a |
B | 8.5≤x<9.0 | 8 |
C | 9.0≤x<9.5 | 15 |
D | 9.5≤x<10 | 3 |

(1)图中a= , 这次比赛成绩的众数落在组;
(2)请补全频数分布直方图;
(3)学校决定选派本次比赛成绩最好的3人参加全市中学生朗诵比赛,并为参赛选手准备了2件白色、1件蓝色上衣和黑色、蓝色、白色的裤子各1条,小军先选,他从中随机选取一件上衣和一条裤子搭配成一套衣服,请用画树状图法或列表法求出上衣和裤子搭配成不同颜色的概率.
参考答案:
【答案】
(1)4;C
(2)解:补全频数分布直方图如下:

(3)解:设两条白色上衣分别记为白1、白2,画出树状图(或列表) 得:
白1 | 白2 | 蓝 | |
黑 | (白1,黑) | (白2,黑) | (蓝,黑) |
蓝 | (白1,蓝) | (白2,蓝) | (蓝,蓝) |
白 | (白1,白) | (白2,白) | (蓝,白) |
由树状图(或表格)可以看出,所有可能出现的结果共有9种,这些结果出现的可能性相等.其中上衣和裤子搭配成不同颜色的结果有6种.
∴P(上衣和裤子搭配成不同颜色)= ![]() =
= ![]()
【解析】解:(1)由条形统计图可知,a=4,由频数分布直方图可知这次比赛成绩的众数落在C组,故答案为:4,C; (1)由条形图可得a的值,根据众数的定义及频数分布表可得答案;(2)根据频数分布表得出B组的频数即可补全条形图;(3)列表法得出所有等可能结果,再根据概率公式可得答案.
-
科目: 来源: 题型:
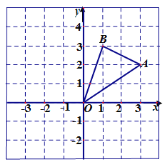
查看答案和解析>>【题目】如图,在边长为1的正方形组成的网格中,三角形AOB的顶点均在格点上,A(3,2),B(1,3),
(1)将三角形AOB先向左平移3个单位长度,后向下平移1个单位得到三角形A1O1B1,请直接作出三角形A1O1B1;
(2)请直接写出三角形A1O1B1三个顶点的坐标;
(3)三角形A1O1B1的面积为_______平方单位.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知购买1盆甲种花卉和3盆乙种花卉共需125元,购买3盆甲种花卉和2盆乙种花卉共需165元.
(1)求购买1盆甲种花卉和购买1盆乙种花卉各需多少元?
(2)某校为绿化校园决定购买甲乙两种花卉共60盆,要求购买的甲种花卉盆数不少于乙种花卉的 ,请帮该校设计一种最省钱的购买方案,并计算此时购买这两种花卉所需的费用.
,请帮该校设计一种最省钱的购买方案,并计算此时购买这两种花卉所需的费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠BAC=30°,AC=4,求菱形OCED的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,一次函数的图象经过点A(2,3)与点B(0,5).
(1)求此一次函数的表达式;
(2)若点P为此一次函数图象上一点,且△POB的面积为10,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),四边形ABCD是平行四边形,BD是它的一条对角线,过顶点A、C分别作AM⊥BD,CN⊥BD,M,N为垂足.
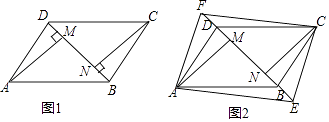
(1)求证:AM=CN;
(2)如图(2),在对角线DB的延长线及反向延长线上分别取点E,F,使BE=DF,连接AE、CF,试探究:当EF满足什么条件时,四边形AECF是矩形?并加以证明.
相关试题

