【题目】如图,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴交于另一点
轴交于另一点![]() .
.
![]() 求此抛物线的解析式;
求此抛物线的解析式;
![]() 已知点
已知点![]() 在第四象限的抛物线上,求点
在第四象限的抛物线上,求点![]() 关于直线
关于直线![]() 对称的点
对称的点![]() 的坐标.
的坐标.
![]() 在
在![]() 的条件下,连接
的条件下,连接![]() ,问在
,问在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() ?若存在,请求出
?若存在,请求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.

参考答案:
【答案】![]()
![]() ;
;![]() 点
点![]() 关于直线
关于直线![]() 对称的点
对称的点![]() ;
;![]() 存在.
存在.![]() ,或
,或![]() .
.
【解析】
(1)将A(-1,0)、C(0,-3)两点坐标代入抛物线y=ax2+bx-3a中,列方程组求a、b的值即可;
(2)将点D(m,-m-1)代入(1)中的抛物线解析式,求m的值,再根据对称性求点D关于直线BC对称的点D'的坐标;
(3)分两种情形①过点C作CP∥BD,交x轴于P,则∠PCB=∠CBD,②连接BD′,过点C作CP′∥BD′,交x轴于P′,
分别求出直线CP和直线CP′的解析式即可解决问题.
![]() 将
将![]() 、
、![]() 代入抛物线
代入抛物线![]() 中,
中,
得![]() ,
,
解得![]() ,
,
∴![]() ;
;
![]() 将点
将点![]() 代入
代入![]() 中,得
中,得
![]() ,
,
解得![]() 或
或![]() ,
,
∵点![]() 在第四象限,
在第四象限,
∴![]() ,
,
∵直线![]() 解析式为
解析式为![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴点![]() 关于直线
关于直线![]() 对称的点
对称的点![]() ;
;
![]() 存在.
存在.
过![]() 点作
点作![]() 轴,垂足为
轴,垂足为![]() ,交直线
,交直线![]() 于
于![]() 点(如图),
点(如图),
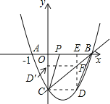
∵![]() ,
,
∴![]() ,
,
又∵![]() 轴,四边形
轴,四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
∴![]() ,
,
设![]() 与
与![]() 相交于
相交于![]() 点
点![]() ,
,
易求![]() 解析式为:
解析式为:![]() ,
,
由![]() ,得到关于
,得到关于![]() 的方程,解方程后,得
的方程,解方程后,得![]() ;
;
于是,![]() 点坐标为:
点坐标为:![]() ;
;
于是![]() 解析式为:
解析式为:![]() ,
,
令![]() 方程中,
方程中,![]() ,则
,则![]() ,
,
所以,![]() 点坐标为:
点坐标为:![]() ,
,
∴![]() ,或
,或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知Rt△ABC中,AC=BC,∠C=90°,D为AB边中点,∠EDF绕D点旋转,它的两边分别交AC、CB(或它们的延长线)于E、F
(1)当点E在AC边上时(如图1),求证CE=BF
(2)在(1)的条件下,求证:

(3)当∠EDF绕D点旋转到图3的位置即点E、F分别在AC、CB边的延长线上时,上述(2)结论是否成立?若成立,请给予证明;若不成立,
 又有怎样的数量关系?请写出你的猜想,不需证明.
又有怎样的数量关系?请写出你的猜想,不需证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙长
 米),用木栏围成三个大小相等的长方形,木栏总长24米,总面积为32平方米.
米),用木栏围成三个大小相等的长方形,木栏总长24米,总面积为32平方米.(1)若墙长
 米,求AB、BC的长.
米,求AB、BC的长.(2)若
 米的墙长对鸡舍的长和宽是否有影响?请说明你的理由.
米的墙长对鸡舍的长和宽是否有影响?请说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,AD∥BC,AE平分∠BAD,点E是CD的中点.
(1)求证:AB=AD+BC
(2)求证:AE⊥BE

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明在一次高尔夫球争霸赛中从山坡上的点
 打出一球向球洞
打出一球向球洞 飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大铅垂高度
飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大铅垂高度 时,球移动的水平距离为
时,球移动的水平距离为 .已知山坡
.已知山坡 与水平方向
与水平方向 的夹角为
的夹角为 ,
, ,
, 两点相距
两点相距
 .
. 求出点
求出点 的坐标;
的坐标; 求抛物线解析式.并判断小明这一杆能否把高尔夫球从点
求抛物线解析式.并判断小明这一杆能否把高尔夫球从点 直接打入球洞
直接打入球洞 ?请说明理由.
?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图9,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,其中A(-2,0),B(-1, -3).

(1)求抛物线的解析式;(3分)
(2)点M为y轴上任意一点,当点M到A、B两点的距离之和为最小时,求此时点M的坐标;(2分)
(3)在第(2)问的结论下,抛物线上的点P使S△PAD=4S△ABM成立,求点P坐标.(4分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在离旗杆6m的A处,用测角仪测得旗杆顶端C的仰角为50°,已知测角仪高AD=1.5m,求旗杆BC的高(结果是近似数,请你自己选择合适的精确度).如果你没有带计算器,也可选用如下:sin50°≈0.7660 cos50≈0.6428 tan50°≈1.192

相关试题

