搜索
【题目】设计一个商标图形（如图8所示），在△ABC中，AB=AC=2cm，∠B=30°，以A为圆心，AB为半径作 
，以BC为直径作半圆 
，则商标图案（阴影）面积等于cm2 ． 
参考答案：
【答案】
+ 
【解析】解：∵S扇形ACB= 
= 
，S半圆CBF= 
π×（ ）2= 
π，S△ABC= ×2 ×1= ； 所以图案面积=S半圆CBF+S△ABC﹣S扇形ACB= π+ ﹣ 
π=（ + ）cm2 ，
所以答案是： + ．
【考点精析】本题主要考查了等腰三角形的性质和扇形面积计算公式的相关知识点，需要掌握等腰三角形的两个底角相等（简称：等边对等角）；在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD的对角线AC和BD交于点O，则下列不能判断四边形ABCD是平行四边形的条件是（ ）
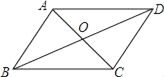
A. OA=OC，AD∥BC B. ∠ABC=∠ADC，AD∥BC
C. AB=DC，AD=BC D. ∠ABD=∠ADB，∠BAO=∠DCO
-
科目： 来源： 题型：
查看答案和解析>>【题目】△ABC的三边为a、b、c，由下列条件不能判断它是直角三角形的是（ ）
A. ∠A: ∠B: ∠C =3∶4∶5 B. ∠A=∠B+∠C
C. a2=(b+c)(b-c) D. a:b:c =1∶2∶
-
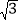
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，tan∠ACD=
，AB=5，那么CD的长是 ． 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，以A点为圆心，以相同的长为半径作弧，分别与射线AM，AN交于B，C两点，连接BC，再分别以B，C为圆心，以相同长（大于
BC）为半径作弧，两弧相交于点D，连接AD，BD，CD．若∠MBD=40°，则∠NCD的度数为_____．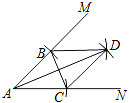
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点A，B在反比例函数y=
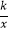（k＞0）的图象上，AC⊥x轴，BD⊥x轴，垂足C，D分别在x轴的正、负半轴上，CD=k，已知AB=2AC，E是AB的中点，且△BCE的面积是△ADE的面积的2倍，则k的值是 ．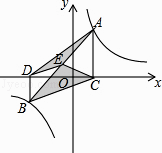 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线，交CE的延长线于点F，且AF=BD，连接BF．
（1）求证：BD=CD；（2）如果AB=AC，试判断四边形AFBD的形状，并证明你的结论．
相关试题
