搜索
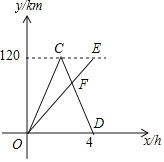
【题目】A、B两地相距120km，甲、乙两车同时从A地出发驶向B地，甲车到达B地后立即按原速返回．如图是它们离A地的距离y(km)与行驶时间x(h)之间的函数图象．
（1）求甲车返回时（即CD段）
与
之间的函数解析式；
（2）若当它们行驶了2.5h时，两车相遇，求乙车的速度及乙车行驶过程中y与x之间的函数解析式，并写出自变量x的取值范围；
（3）直接写出当两车相距20km时，甲车行驶的时间．
参考答案：
【答案】（1）
（2）
（3）
【解析】
（1）根据题意和函数图象中的数据可以求得甲车返回时（即CD段）y与x之间的函数解析式；
（2）根据题意和函数图象中的数据可以求得当它们行驶了2.5h时，两车相遇，求乙车的速度及乙车行驶过程中y与x之间的函数解析式，并写出自变量x的取值范围；
（3）根据题意可以列出相应的方程，求出当两车相距20km时，甲车行驶的时间．
（1）由题意可得，点C的坐标为
，点D的坐标为
设甲车返回时（即CD段）y与x之间的函数解析式为
，代入点C、D可得
解得
即甲车返回时（即CD段）y与x之间的函数解析式为；
（2）将
代入，得
∴点F的坐标为
∴乙车的速度为
，乙车从A地到B地用的时间为
设一车行驶过程中y与x的函数解析式为
代入点F可得
解得
即乙车的速度是
，乙车行驶过程中y与x之间的函数解析式为；
（3）设OC段对应的函数解析式为
，代入点C可得
解
即OC段对应的函数解析式为
解得
解得
故答案为：．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在直角坐标系中，我们把横、纵坐标都为整数的点叫做整点，设坐标轴的单位长度为1cm， 整点P从原点0出发，速度为1cm/s, 且整点P做向上或向右运动(如图1所示.运动时间(s)与整点(个)的关系如下表:
整点P从原点出发的时间(s)
可以得到整点P的坐标
可以得到整点P的个数
1
(0，1)（1，0）
2
2
(0，2)（1，1）(2,0)
3
3
(0,3)(1,2)(2,1)(3,0)
4
.
·
.
根据上表中的规律，回答下列问题:
（1）当整点P从点0出发4s时，可以得到的整点的个数为______个.
（2）当整点P从点O出发8s时，在直角坐标系中描出可以得到的所有整点,并顺次连结这些整点.
（3）当整点P从点0出发______s时，可以得到整点(16,4)的位置.
-
科目： 来源： 题型：
查看答案和解析>>【题目】2019年4月23日世界读书日这天，滨江初二年级的学生会，就2018年寒假读课外书数量（单位：本）做了调查，他们随机调查了甲、乙两个班的10名同学，调查过程如下
收集数据
甲、乙两班被调查者读课外书数量（单位：本）统计如下：
甲：1，9，7，4，2，3，3，2，7，2
乙：2，6，6，3，1，6，5，2，5，4
整理、描述数据绘制统计表如下，请补全下表：
班级
平均数
众数
中位数
方差
甲
4
3
乙
6
3.2
分析数据、推断结论
（1）该校初二乙班共有40名同学，你估计读6本书的同学大概有_____人；
（2）你认为哪个班同学寒假读书情况更好，写出理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣2tx+t2﹣2t+4＝0．
（1）当t＝3时，解这个方程；
（2）若m，n是方程的两个实数根，设Q＝（m﹣2）（n﹣2），试求Q的最小值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在正方形ABCD中，P是对角线BD上的一点，点E在AD的延长线上，且PA=PE，PE交CD于F．
（1）证明：PC=PE；
（2）求∠CPE的度数；
（3）如图2，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC=120°时，连接CE，试探究线段AP与线段CE的数量关系，并说明理由．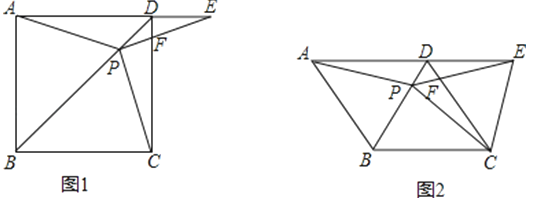
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义：我们把对角线互相垂直的四边形叫做垂美四边形．
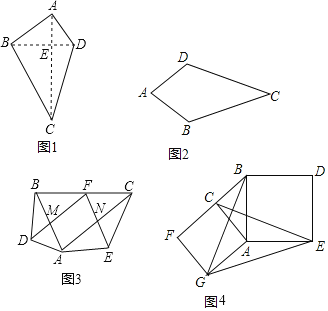
（1）概念理解：如图2，在四边形ABCD中，AB=AD，CB=CD，那么四边形ABCD是垂美四边形吗？请说明理由．
（2）性质探究：
①如图1，垂美四边形ABCD两组对边AB、CD与BC、AD之间有怎样的数量关系？写出你的猜想，并给出证明．
②如图3，在Rt△ABC中，点F为斜边BC的中点，分别以AB，AC为底边，在
外部作等腰三角形ABD和等腰三角形ACE，连接FD，FE，分别交AB，AC于点M，N．试猜想四边形FMAN的形状，并说明理由；（3）问题解决：
如图4，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE、BG，GE，已知AC=2，AB=5．求GE的长度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知在正方形ABCD中，AE∥BD，BE=BD，BE交AD于F．求证：DE=DF．
相关试题
