【题目】定义:我们把对角线互相垂直的四边形叫做垂美四边形.
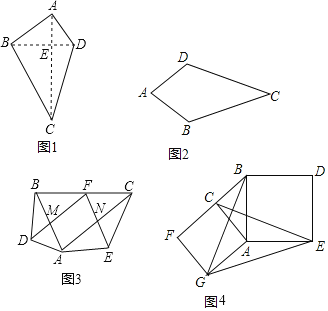
(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,那么四边形ABCD是垂美四边形吗?请说明理由.
(2)性质探究:
①如图1,垂美四边形ABCD两组对边AB、CD与BC、AD之间有怎样的数量关系?写出你的猜想,并给出证明.
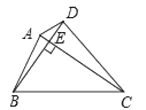
②如图3,在Rt△ABC中,点F为斜边BC的中点,分别以AB,AC为底边,在![]() 外部作等腰三角形ABD和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN的形状,并说明理由;
外部作等腰三角形ABD和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN的形状,并说明理由;
(3)问题解决:
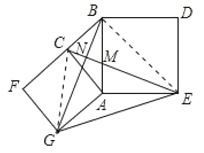
如图4,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE、BG,GE,已知AC=2,AB=5.求GE的长度.
参考答案:
【答案】(1)四边形ABCD是垂美四边形,证明见解析 (2)①![]() ,证明见解析;②四边形FMAN是矩形,证明见解析 (3)
,证明见解析;②四边形FMAN是矩形,证明见解析 (3)![]()
【解析】
(1)根据垂直平分线的判定定理证明即可;
(2)①根据垂直的定义和勾股定理解答即可;②根据在Rt△ABC中,点F为斜边BC的中点,可得![]() ,再根据△ABD和△ACE是等腰三角形,可得
,再根据△ABD和△ACE是等腰三角形,可得![]() ,再由(1)可得,
,再由(1)可得,![]() ,从而判定四边形FMAN是矩形;
,从而判定四边形FMAN是矩形;
(3)根据垂美四边形的性质、勾股定理、结合(2)的结论计算即可.
(1)四边形ABCD是垂美四边形
连接AC、BD
∵![]()
∴点A在线段BD的垂直平分线上
∵![]()
∴点C在线段BD的垂直平分线上
∴直线AC是线段BD的垂直平分线
∴![]()
∴四边形ABCD是垂美四边形;
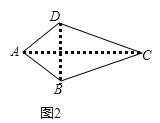
(2)①![]() ,理由如下
,理由如下
如图,已知四边形ABCD中,![]() ,垂足为E
,垂足为E
![]()
![]()
由勾股定理得
![]()
![]()
![]()
②四边形FMAN是矩形,理由如下
如图,连接AF

∵在Rt△ABC中,点F为斜边BC的中点
![]()
∵△ABD和△ACE是等腰三角形
![]()
由(1)可得,![]()
∵![]()
![]()
∴四边形FMAN是矩形;
(3)连接CG、BE,
![]()
![]() ,即
,即![]()
在△AGB和△ACE中
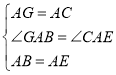
![]()
![]()
∵![]()
![]() ,即
,即![]()
∴四边形CGEB是垂美四边形
由(2)得![]()
![]()
![]()
![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣2tx+t2﹣2t+4=0.
(1)当t=3时,解这个方程;
(2)若m,n是方程的两个实数根,设Q=(m﹣2)(n﹣2),试求Q的最小值.
-
科目: 来源: 题型:
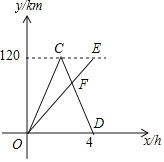
查看答案和解析>>【题目】A、B两地相距120km,甲、乙两车同时从A地出发驶向B地,甲车到达B地后立即按原速返回.如图是它们离A地的距离y(km)与行驶时间x(h)之间的函数图象.
(1)求甲车返回时(即CD段)
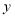 与
与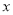 之间的函数解析式;
之间的函数解析式;(2)若当它们行驶了2.5h时,两车相遇,求乙车的速度及乙车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(3)直接写出当两车相距20km时,甲车行驶的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.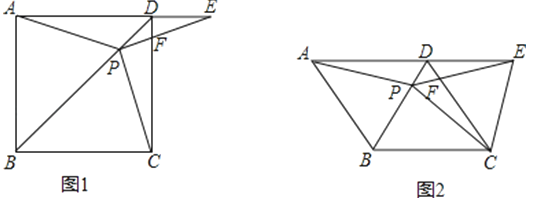
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在正方形ABCD中,AE∥BD,BE=BD,BE交AD于F.求证:DE=DF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,AD∥BC,要判别四边形ABCD是平行四边形,还需满足条件( )
A. ∠A+∠C=180°B. ∠B+∠D=180°
C. ∠A+∠B=180°D. ∠A+∠D=180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】对非负实数x“四舍五入”到个位的值记为[x].即当n为非负整数时,若n﹣
 ≤x<n+
≤x<n+  ,则[x]=n.如:[3.4]=3,[3.5]=4,…根据以上材料,解决下列问题:
,则[x]=n.如:[3.4]=3,[3.5]=4,…根据以上材料,解决下列问题: (1)填空:
①若[x]=3,则x应满足的条件:________;
②若[3x+1]=3,则x应满足的条件:________;
(2)求满足[x]=
 x﹣1的所有非负实数x的值.
x﹣1的所有非负实数x的值.
相关试题

