【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,求抛物线经过A(1,0),C(0,3)两点,与x轴交于A、B两点.
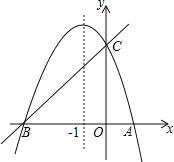
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在该抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为该抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.(提示:若平面直角坐标系内两点P(x1,y1)、Q(x2,y2),则线段PQ的长度PQ=![]() ).
).
参考答案:
【答案】(1)直线的解析式是y=x+3;抛物线的解析式是y=﹣x2﹣2x+3;(2)M的坐标是(﹣1,2);(3)P的坐标是(﹣1,﹣1)或(﹣1,2)或(﹣1,4)或(﹣1,﹣2).
【解析】
试题分析:(1)根据A和B关于x=﹣1对称即可求得B的坐标,然后利用待定系数法即可求得抛物线的解析式;
(2)求得BC与对称轴的交点就是M;
(3)设P的坐标是(﹣1,p),利用两点之间的距离公式表示出BC、BP和PC的长,然后分成△BPC的三边分别是斜边三种情况讨论,利用勾股定理列方程求得p的值,得到P的坐标.
解:(1)A(1,0)关于x=﹣1的对称点是(﹣3,0),则B的坐标是(﹣3,0).
根据题意得:![]() ,
,
解得:![]() ,
,
则抛物线的解析式是y=x+3;
根据题意得: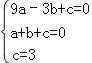 ,
,
解得: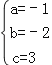 .
.
则抛物线的解析式是y=﹣x2﹣2x+3;
(2)在y=x+3中令x=﹣1,则y=﹣1+3=2,
则M的坐标是(﹣1,2);
(3)设P的坐标是(﹣1,p).
则BP2=(﹣1+3)2+p2=4+p2.
PC=(0+1)2+(3﹣p)2=p2﹣6p+10.
BC=32+32=18.
当BC时斜边时,BP2+PC2=BC2,则(4+p2)+(p2﹣6p+10)=18,
解得:p=﹣1或2,
则P的坐标是(﹣1,﹣1)或(﹣1,2);
当BP是斜边时,BP2=PC2+BC2,则4+p2=(p2﹣6p+10)+18,
解得:p=4,
则P的坐标是(﹣1,4);
当PC是斜边时,PC2=BP2+BC2,则p2﹣6p+10=4+p2+18,
解得:p=﹣2,
则P的坐标是(﹣1,﹣2).
总之,P的坐标是(﹣1,﹣1)或(﹣1,2)或(﹣1,4)或(﹣1,﹣2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.

(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 填空题:如图,AB//CD,∠ABC=50°,∠CPN=150°,∠PNB=60°,∠NDC=60°,求∠BCP的度数。

解:
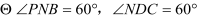 ,(已知)
,(已知)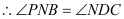 ,(等量代换)
,(等量代换) PN // CD,( )
PN // CD,( )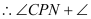 _________=180°,( )
_________=180°,( )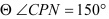 ,(已知)
,(已知)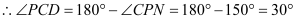
 ,(已知)
,(已知)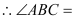
 ____________,(两直线平行,内错角相等)
____________,(两直线平行,内错角相等)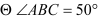 ,(已知)
,(已知) __________,(等量代换)
__________,(等量代换)
 BCP=
BCP= BCD-
BCD- PCD=____________°-30°=_________°.
PCD=____________°-30°=_________°. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知2a-1的平方根是±3,3a-b+2的算术平方根是4,求a+3b的立方根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD与AB,CD交于A,D两点,EC,BF与AB,CD交于E,C,B,F,且∠1=∠2,∠B=∠C,
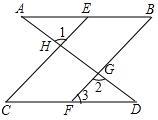
(1)说明CE∥BF.
(2)你能得出∠B=∠3和∠A=∠D这两个结论吗?若能,写出你得出结论的过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),△ABC是一个三角形的纸片,点D、E分别是△ABC边上的两点,
研究(1):如果沿直线DE折叠,则∠BDA′与∠A的关系是 .
研究(2):如果折成图2的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由.
研究(3):如果折成图3的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=﹣x2+x+2,则当y<0时,自变量x的取值范围是( )
A.x<﹣1或x>2 B.﹣1<x<2
C.x<﹣2或x>1 D.﹣2<x<1
相关试题

