【题目】 填空题:如图,AB//CD,∠ABC=50°,∠CPN=150°,∠PNB=60°,∠NDC=60°,求∠BCP的度数。

解:![]() ,(已知)
,(已知)
![]() ,(等量代换)
,(等量代换)
![]() PN // CD,( )
PN // CD,( )
![]() _________=180°,( )
_________=180°,( )
![]() ,(已知)
,(已知)
![]()
![]() ,(已知)
,(已知)
![]()
![]() ____________,(两直线平行,内错角相等)
____________,(两直线平行,内错角相等)
![]() ,(已知)
,(已知)
![]() __________,(等量代换)
__________,(等量代换)
![]()
![]() BCP=
BCP=![]() BCD-
BCD-![]() PCD=____________°-30°=_________°.
PCD=____________°-30°=_________°.
参考答案:
【答案】PN,CD,(同位角相等,两直线平行),PCD,(两直线平行,同旁内角互补),BCD,(两直线平行,内错角相等),50°,50,30,20.∠CPN∠PCN
【解析】
试题分析:根据平行线的判定推出PN∥CD,推出∠CPN+∠PCD=180°,求出∠PCD=30°,根据平行线性质得出∠ABC=∠BCD,求出∠BCD=50°,代入∠BCP=∠BCD-∠PCD求出即可.
试题解析:∵∠PNB=60°,∠NDC=60°,
∴∠PNB=∠NDC,(等量代换),
∴PN∥CD,(同位角相等,两直线平行),
∴∠CPN+∠PCD=180°,(两直线平行,同旁内角互补)
∵∠CPN=150°,
∴∠PCD=30°,
∵AB∥CD,(已知)
∴∠ABC=∠BCD,(两直线平行,内错角相等)
∵∠ABC=50°,(已知)
∴∠BCD=50°,(等量代换)
∴∠BCP=∠BCD-∠PCD=50°-30°=20°
-
科目: 来源: 题型:
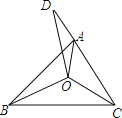
查看答案和解析>>【题目】如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO,若∠BAC=92°,则∠BCA的度数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和是外角和的3倍,这个多边形的边数是( )
A. 7 B. 8 C. 9 D. 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.

(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知2a-1的平方根是±3,3a-b+2的算术平方根是4,求a+3b的立方根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,求抛物线经过A(1,0),C(0,3)两点,与x轴交于A、B两点.
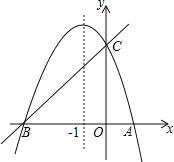
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在该抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为该抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.(提示:若平面直角坐标系内两点P(x1,y1)、Q(x2,y2),则线段PQ的长度PQ=
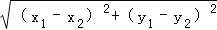 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD与AB,CD交于A,D两点,EC,BF与AB,CD交于E,C,B,F,且∠1=∠2,∠B=∠C,
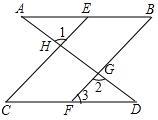
(1)说明CE∥BF.
(2)你能得出∠B=∠3和∠A=∠D这两个结论吗?若能,写出你得出结论的过程.
相关试题

