【题目】如图,已知AD与AB,CD交于A,D两点,EC,BF与AB,CD交于E,C,B,F,且∠1=∠2,∠B=∠C,
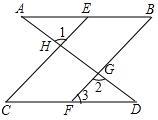
(1)说明CE∥BF.
(2)你能得出∠B=∠3和∠A=∠D这两个结论吗?若能,写出你得出结论的过程.
参考答案:
【答案】(1)说明见解析;(2)能,理由如下.
【解析】
试题分析:(1)根据对顶角相等得到∠1=∠CHG,又∠1=∠2,则∠CHG=∠2,根据“同位角相等,两直线平行”即可得到结论;
(2)由CE∥BF,根据“两直线平行,同位角相等”得∠C=∠3,而∠B=∠C,则∠B=∠3,根据平行线的判定得AB∥CD,然后根据平行线的性质即可得到∠A=∠D.
试题解析:(1)∵∠1=∠CHG,
又∠1=∠2,
∴∠CHG=∠2,
∴CE∥BF;
(2)能.理由如下:
∵CE∥BF,
∴∠C=∠3,
而∠B=∠C,
∴∠B=∠3,
∴AB∥CD,
∴∠A=∠D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 填空题:如图,AB//CD,∠ABC=50°,∠CPN=150°,∠PNB=60°,∠NDC=60°,求∠BCP的度数。

解:
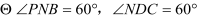 ,(已知)
,(已知)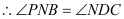 ,(等量代换)
,(等量代换) PN // CD,( )
PN // CD,( )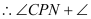 _________=180°,( )
_________=180°,( )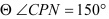 ,(已知)
,(已知)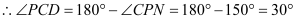
 ,(已知)
,(已知)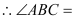
 ____________,(两直线平行,内错角相等)
____________,(两直线平行,内错角相等)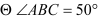 ,(已知)
,(已知) __________,(等量代换)
__________,(等量代换)
 BCP=
BCP= BCD-
BCD- PCD=____________°-30°=_________°.
PCD=____________°-30°=_________°. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知2a-1的平方根是±3,3a-b+2的算术平方根是4,求a+3b的立方根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,求抛物线经过A(1,0),C(0,3)两点,与x轴交于A、B两点.
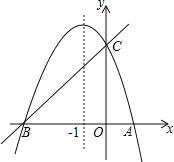
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在该抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为该抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.(提示:若平面直角坐标系内两点P(x1,y1)、Q(x2,y2),则线段PQ的长度PQ=
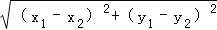 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),△ABC是一个三角形的纸片,点D、E分别是△ABC边上的两点,
研究(1):如果沿直线DE折叠,则∠BDA′与∠A的关系是 .
研究(2):如果折成图2的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由.
研究(3):如果折成图3的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=﹣x2+x+2,则当y<0时,自变量x的取值范围是( )
A.x<﹣1或x>2 B.﹣1<x<2
C.x<﹣2或x>1 D.﹣2<x<1
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a2a3=a6 B.a2+a2=a4 C.3a2×2a2=6a4 D.5a﹣a=4
相关试题

