【题目】为了推动阳光体育运动的广泛开展,引导学生走向操场,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了统计图①和图②,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为______,图①中![]() 的值为_____;
的值为_____;
(2)本次调查获取的样本数据的众数为______,中位数为________;
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?

参考答案:
【答案】 40 15 众数35号 中位数36号
【解析】试题分析:(1)由图②可得36号有10人,由图①可得36号占样本比例为25%,所以样本总数为![]() ,因为事件的概率和为1,所以m%=100%-30%-25%-20%-10%=15%,所以m的值为15.
,因为事件的概率和为1,所以m%=100%-30%-25%-20%-10%=15%,所以m的值为15.
(2)由图②可得35号数量最多,所以众数为35,将这组样本数据从小到大的顺序排列,其中处于中间的两个数都为36,所以中位数为36,
(3)根据样本得出35号鞋的概率,以此概率估算全校.
试题解析:(1)本次接受随机抽样调查的学生人数为6+12+10+8+4=40,图①中m的值为100-30-25-20-10=1,
故答案为:40,15,
(2)∵在这组样本数据中,35出现了12次,出现次数最多,
∴这组样本数据的众数为35,
∵将这组样本数据从小到大得顺序排列,其中处于中间的两个数都为36,
∴中位数为![]() =36,
=36,
(3)∵在40名学生中,鞋号为35的学生人数比例为30%,
∴由样本数据,估计学校各年级中学生鞋号为35的人数比例约为30%,
则计划购买200双运动鞋,有200×30%=60双为35号.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC是等腰三角形,AB=AC,点D,E,F分别在AB,BC,AC边上,且BD=CE,BE=CF.
(1)求证:△DEF是等腰三角形;
(2)猜想:当∠A满足什么条件时,△DEF是等边三角形?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点 A(0,4)在 y 轴上,点 B(b,0)是 x 轴上一动点,且 4< b <4,△ABC 是以 AB 为直角边,B 为直角顶点的等腰直角三角形.
(1)求点 C 的坐标(用含 b 的式子表示);
(2)以 x 轴为对称轴,作点 C 的对称点 C 连接 BC、AC,请把图形补充完整,并求出△ABC的面积(用含 b 的式子表示);
(3)点 B 在运动过程中, OAC 的度数是否发生变化,若变化请说明理由;若不变化,请直接 写出 OAC 的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小明遇到这样一个问题:如图 1,在四边形 ABCD 中,E 是 BC 的中点,AE 是∠BAD 的平分线,AB∥DC,求证:AD=AB+DC. 小明发现以下两种方法:
方法 1:如图 2,延长 AE、DC 交于点 F;
方法 2:如图 3,在 AD 上取一点 G 使 AG=AB,连接 EG、CG.
(1)根据阅读材料,任选一种方法,证明:AD=AB+DC; 用学过的知识或参考小明的方法,解决下面的问题:
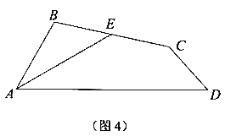
(2)如图 4,在四边形 ABCD 中,AE 是∠BAD 的平分线,E 是 BC 的中点,∠BAD=60°,∠ABC=180°-
 ∠BCD,求证:CD=CE.
∠BCD,求证:CD=CE.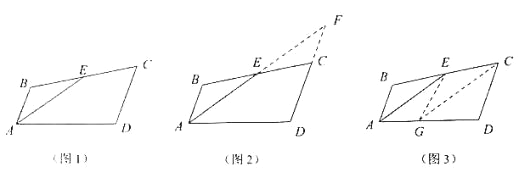
-
科目: 来源: 题型:
查看答案和解析>>【题目】为方便市民通行,某广场计划对坡角为30°,坡长为60米的斜坡AB进行改造,在斜坡中点D处挖去部分坡体(阴影表示),修建一个平行于水平线CA的平台DE和一条新的斜坡BE.
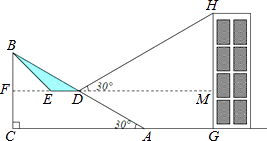
(1)若修建的斜坡BE的坡角为36°,则平台DE的长约为多少米?
(2)在距离坡角A点27米远的G处是商场主楼,小明在D点测得主楼顶部H 的仰角为30°,那么主楼GH高约为多少米?(结果取整数,参考数据:sin36°=0.6,cos36°=0.8,tan36°=0.7,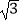 =1.7)
=1.7) -
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形 ABCD 中,BC=CD,连接 AC、BD,∠ADB=90°.
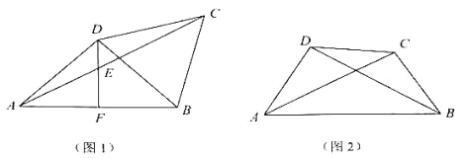
(1)如图 1,若 AD=BD=BC,过点 D 作 DF⊥AB 于点 F,交 AC 于点 E:
①求∠DAC;
②猜想 AE、DE、CE 的数量关系,并证明你的猜想;
(2)如图 2,若 AC=BD,求∠DAC 的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,我们把横 、纵坐标都是整数的点叫做整点.已知点
中,我们把横 、纵坐标都是整数的点叫做整点.已知点A(0,4),点B是
 轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)
轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)
相关试题

