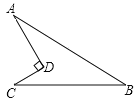
【题目】如图,有一块四边形花圃ABCD,∠ADC=90°,AD=4m,AB=13m,BC=12m,DC=3m,求该花圃的面积.
参考答案:
【答案】24m2
【解析】试题分析: 连接AC,先利用勾股定理求AC,再利用勾股定理逆定理证△ACB为直角三角形,根据四边形ABCD的面积=△ABC面积-△ACD面积即可计算.
试题解析:
连接AC,
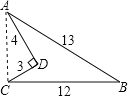
∵AD=4m,CD=3m,∠ADC=90°,
∴AC=5m,
△ACD的面积=12×3×4=6(m),
在△ABC中,
∵AC=5m,BC=12m,AB=13m,
∴AC+BC=AB,
∴△ABC为直角三角形,且∠ACB=90°,
∴直角△ABC的面积=12×12×5=30(m),
∴四边形ABCD的面积=306=24(m).
∴该花圃的面积是24m2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算结果为m6的是( )
A.m2+m3
B.m2m3
C.(﹣m2)3
D.m9÷m3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
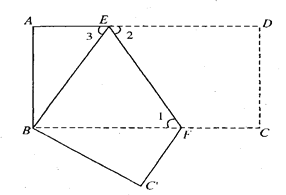
(1)折叠后,DC的对应线段是 ,CF的对应线段是 ;
(2)若∠1=50°,求∠2、∠3的度数;
(3)若CD=4,AD=6,求CF的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将容量为100的样本分成3个组,第一组的频数是35,第二组的频率是0.28,那么第三组的频率是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xoy中,点A、B、C的坐标分别为(-1,0)、(-2,3)、(-3,1).
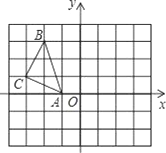
(1)作出△ABC关于x轴对称的 △A1B1C1,并写出B1、C1
两点的坐标:B1: , C1: .
(2)△ABC的面积S△ABC= .
(3)若D点在y轴上运动,求CD+DA的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组线段能组成一个三角形的是( )
A.4cm,6cm,11cm
B.4cm,5cm,1cm
C.3cm,4cm,5cm
D.2cm,3cm,6cm -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)发现:
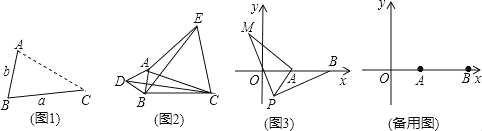
如图1,点A为线段BC外一动点,且BC=a,AB=b.
填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a,b的式子表示)
(2)应用:
点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.
(3)拓展:
如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.
相关试题

