搜索
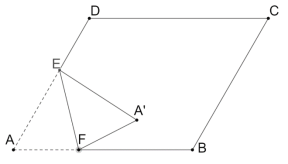
【题目】如图,在菱形
中，
, 
, 点
在边
上,且
，点
为线段
上一动点(不与点
重合),将菱形沿直线
折叠，点的对应点为点
，当落在菱形的对角线上时，
的长为__________．
参考答案：
【答案】2或
【解析】
分为两种情况:当点
在BD上时和当点;在AC上时，再利用菱形的性质和等边三角形的性质进行解答．
①当点在BD上时，如图:
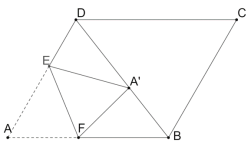
则
，
，FA=F
∴
∵四边形ABCD是菱形
∴AB=AD=3
∵
∴△ABD为等边三角形，
∴
∴
∴
∴
∵DE=1
∴
设AF=
=x， 
解得x=
∴AF=
②当点在AC上时，如图:
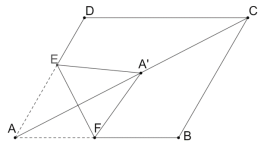
则EF垂直平分
∵四边形ABCD是蒙形，∠DAB=60°
∴∠DAC=∠CBA=30，∠AFE=∠DAB=60°
∴AF=AE=2
综上所述:AF=2或
故答案为：2或
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，O为坐标原点，△AOB是等腰直角三角形，∠AOB=90°，点A（2,1）.
（1）求点B的坐标；
（2）求经过A、O、B三点的抛物线的函数表达式；
（3）在（2）所求的抛物线上，是否存在一点P，使四边形ABOP的面积最大？若存在，求出点P的坐标；若不存在，请说明理由.
-
科目： 来源： 题型：
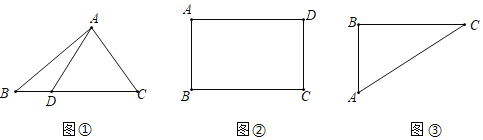
查看答案和解析>>【题目】问题提出（1）如图①，在△ABC中，BC＝6，D为BC上一点，AD＝4，则△ABC面积的最大值是 ．
问题探究（2）如图②，已知矩形ABCD的周长为12，求矩形ABCD面积的最大值．
问题解决（3）如图③，△ABC是葛叔叔家的菜地示意图，其中AB＝30米，BC＝40米，AC＝50米，现在他想利用周边地的情况，把原来的三角形地拓展成符合条件的面积尽可能大、周长尽可能长的四边形地，用来建鱼塘．已知葛叔叔欲建的鱼塘是四边形ABCD，且满足∠ADC＝60°．你认为葛叔叔的想法能否实现？若能，求出这个四边形鱼塘周长的最大值；若不能，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数
(
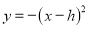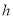为常数)，当自变量
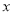的值满足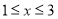
时，其对应的函数值
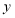的最大值为
,则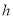的值为 （ ）A.2或4B.0或-4C.2或-4D.0或4
-
科目： 来源： 题型：
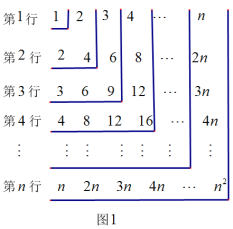
查看答案和解析>>【题目】如图1，观察数表，如何计算数表中所有数的和?
方法1：如图1，先求每行数的和：
第1行
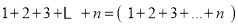
第2行
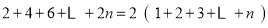
第n行
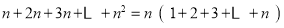
故表中所有数的和：
；
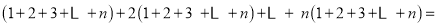方法2：如图2．依次以第1行每个数为起点，按顺时针方向计算各数的和：
第1组
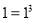
第2组
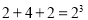
第3组
…
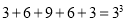
第
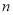组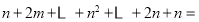 
，用这
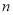组数计算的结果，表示数表中所有数的和为： ，综合上面两种方法所得的结果可得等式： ；
利用上面得到的规律计算：
．
-
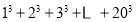科目： 来源： 题型：
查看答案和解析>>【题目】将正面分别标有数字-1、2、3、4的四张卡片(除数字外其余都相同)洗匀后,背面朝上放置在桌面上.
（1）小明从这四张卡片中随机抽取一张， 抽到一张恰好是负数的概率是多少?
（2）随机抽出一张，记其数字为
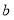,不放回,再随机抽出一张， 记其数字为
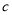,则使关于
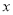的方程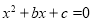
有实数根的概率是多少? -
科目： 来源： 题型：
查看答案和解析>>【题目】“淮南牛肉汤”是安徽知名地方小吃．某分店经理发现，当每碗牛肉汤的售价为6元时，每天能卖出500碗；当每碗牛肉汤的售价每增加0.5元时，每天就会少卖出20碗，设每碗牛肉汤的售价增加
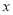元时，一天的营业额为
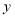元．（1）求
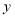与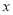的函数关系式（不要求写出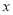的取值范围）；（2）考虑到顾客可接受价格
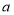元/碗的范围是
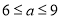，且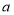为整数，不考虑其他因素，则该分店的牛肉汤每碗多少元时，每天的牛肉汤营业额最大？最大营业额是多少元？
相关试题
