【题目】“淮南牛肉汤”是安徽知名地方小吃.某分店经理发现,当每碗牛肉汤的售价为6元时,每天能卖出500碗;当每碗牛肉汤的售价每增加0.5元时,每天就会少卖出20碗,设每碗牛肉汤的售价增加![]() 元时,一天的营业额为
元时,一天的营业额为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式(不要求写出
的函数关系式(不要求写出![]() 的取值范围);
的取值范围);
(2)考虑到顾客可接受价格![]() 元/碗的范围是
元/碗的范围是![]() ,且
,且![]() 为整数,不考虑其他因素,则该分店的牛肉汤每碗多少元时,每天的牛肉汤营业额最大?最大营业额是多少元?
为整数,不考虑其他因素,则该分店的牛肉汤每碗多少元时,每天的牛肉汤营业额最大?最大营业额是多少元?
参考答案:
【答案】(1) ![]() ;(2)售价为9元每碗时,每天的最大营业额为3420元
;(2)售价为9元每碗时,每天的最大营业额为3420元
【解析】
(1)根据题意:售价×碗数=一天的营业额=(6+x)(500-20×![]() )
)
(2)由(1)可得当![]() 时
时![]() 随着
随着![]() 的增大而增大,再结合x取整数,即可解答,将x=3代入函数关系式可得最大营业额
的增大而增大,再结合x取整数,即可解答,将x=3代入函数关系式可得最大营业额
(1) ![]()
(2) 由(1)得![]() ,
,![]() ,当
,当![]() 时
时![]() 随着
随着![]() 的增大而增大,又
的增大而增大,又![]() ,结合
,结合![]() 为整数,故当
为整数,故当![]() ,即售价为9元每碗时,每天的最大营业额为3420元
,即售价为9元每碗时,每天的最大营业额为3420元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
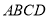 中,
中,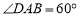 ,
,  , 点
, 点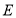 在边
在边 上,且
上,且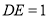 ,点
,点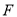 为线段
为线段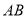 上一动点(不与点
上一动点(不与点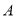 重合),将菱形沿直线
重合),将菱形沿直线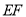 折叠,点
折叠,点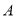 的对应点为点
的对应点为点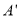 ,当
,当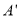 落在菱形的对角线上时,
落在菱形的对角线上时,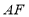 的长为__________.
的长为__________.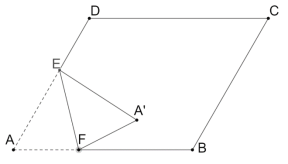
-
科目: 来源: 题型:
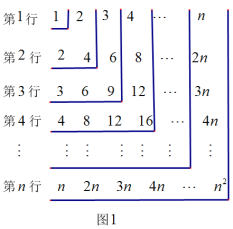
查看答案和解析>>【题目】如图1,观察数表,如何计算数表中所有数的和?
方法1:如图1,先求每行数的和:
第1行
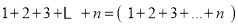
第2行
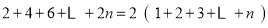
第n行
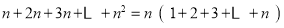
故表中所有数的和:
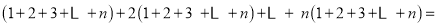 ;
;
方法2:如图2.依次以第1行每个数为起点,按顺时针方向计算各数的和:
第1组
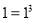
第2组
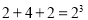
第3组
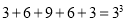
…
第
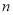 组
组 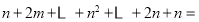 ,
,用这
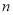 组数计算的结果,表示数表中所有数的和为: ,
组数计算的结果,表示数表中所有数的和为: ,综合上面两种方法所得的结果可得等式: ;
利用上面得到的规律计算:
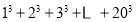 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将正面分别标有数字-1、2、3、4的四张卡片(除数字外其余都相同)洗匀后,背面朝上放置在桌面上.
(1)小明从这四张卡片中随机抽取一张, 抽到一张恰好是负数的概率是多少?
(2)随机抽出一张,记其数字为
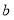 ,不放回,再随机抽出一张, 记其数字为
,不放回,再随机抽出一张, 记其数字为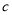 ,则使关于
,则使关于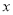 的方程
的方程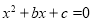 有实数根的概率是多少?
有实数根的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 边长为2,
边长为2, 、
、 分别是
分别是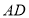 、
、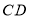 上两动点,且满足
上两动点,且满足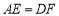 ,
, 交
交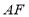 于点
于点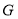 .
.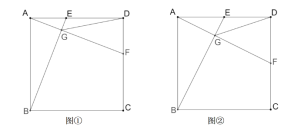
(1)如图1,判断线段
 、
、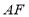 的位置关系,并说明理由;
的位置关系,并说明理由;(2)在(1)的条件下,连接
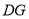 ,直接写出
,直接写出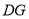 的最小值为 ;
的最小值为 ;(3)如图2,点
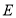 为
为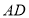 的中点,连接
的中点,连接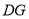 .
.①求证:
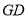 平分
平分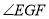 ;
;②求线段
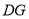 的长度.
的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=BC=3cm.动点P从点A出发,以
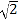 cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC
cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是 ( )
CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是 ( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
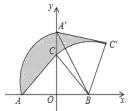
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC=2,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角线坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴正半轴上的A′处,则图中阴影部分面积为_____.
相关试题

