【题目】在△ABC中,∠C=90°,AC=BC.作射线AP,过点B作BD⊥AP于点D,连接CD.
(1)当射线AP位于图1所示的位置时
①根据题意补全图形;
②求证:AD+BD=![]() CD.
CD.
(2)当射线AP绕点A由图1的位置顺时针旋转至∠BAC的内部,如图2,直接写出此时AD,BD,CD三条线段之间的数量关系为 .

参考答案:
【答案】(1)①见解析;②见解析;(2)结论:AD﹣BD= CD.理由见解析.
【解析】
(1)①根据要求补全图形即可;
②取AB是中点O,连接OD、OC,作CE⊥AD于E,CF⊥DB于F.四只要证明边形DECF是正方形,可得DE=DF,CD= ![]() DE
DE
由Rt△CAE≌Rt△CBF,推出AE=BF,可得AB+DB=DE+AE+DF-BF=2DE,
(2)结论:AD-BD= ![]() CD,取AB的中点O,连接OC,OD.作CM⊥CD交AD于M.只要证明△MCD是等腰直角三角形,△ACM≌△BCD,、即可解决问题;
CD,取AB的中点O,连接OC,OD.作CM⊥CD交AD于M.只要证明△MCD是等腰直角三角形,△ACM≌△BCD,、即可解决问题;
(1)解:①补全图的图形如图所示;
②证明:取AB是中点O,连接OD、OC,作CE⊥AD于E,CF⊥DB于F.
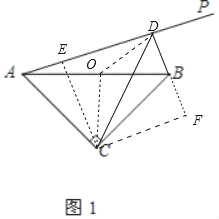
∵∠ACB=∠ADB=90°,
∴OC=OD=![]() AB,
AB,
∴A、D、B、C四点共圆,
∴∠ADB=∠ABC=45°,
∴∠ADC=∠CDB,
∵CE⊥AD于E,CF⊥DB于F,
∴CE=CF,
易证四边形DECF是正方形,
∴DE=DF,CD=![]() DE,
DE,
∵AC=BC,CE=CF,
∴Rt△CAE≌Rt△CBF,
∴AE=BF,
∵AB+DB=DE+AE+DF﹣BF=2DE,
又∵DE=![]() CD,
CD,
∴AB+BD=![]() CD.
CD.
(2)结论:AD﹣BD=![]() CD.
CD.
理由:取AB的中点O,连接OC,OD.作CM⊥CD交AD于M.
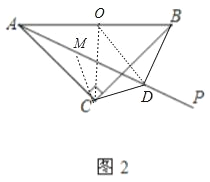
∵∠ACB=∠ADB=90°,OA=OB,
∴OC=OD=![]() AB,
AB,
∴A、C、D、B四点共圆,(设AD交BC于O,先证明△AOC∽△BOD,再证明△AOB∽△COD即可)
∴∠ADC=∠ABC=45°,
∴△MCD是等腰直角三角形,
∴CM=CD,
∵∠MCD=∠ACB=90°,
∴∠ACM=∠BCD,∵CA=CB,
∴△ACM≌△BCD,
∴AM=BD,
∴AD﹣BD=AD=AM=DM=![]() CD.
CD.
故答案为:AD﹣BD=![]() CD.
CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某镇水库的可用水量为12000万立方米,假设年降水量不变,能维持该镇16万人20年的用水量.实施城市化建设,新迁入4万人后,水库只够维持居民15年的用水量.
(1)问:年降水量为多少万立方米?每人年平均用水量多少立方米?
(2)政府号召节约用水,希望将水库的保用年限提高到25年,则该镇居民人均每年需节约多少立方米才能实现目标? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线y=
 (x﹣m)2﹣
(x﹣m)2﹣  m2+m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.
m2+m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.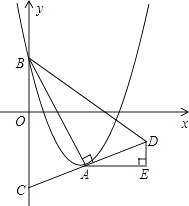
(1)当m=2时,求点B的坐标;
(2)求DE的长?
(3)①设点D的坐标为(x,y),求y关于x的函数关系式?②过点D作AB的平行线,与第(3)①题确定的函数图象的另一个交点为P,当m为何值时,以A,B,D,P为顶点的四边形是平行四边形? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(﹣
 ,3 ),AB=2,AD=3.
,3 ),AB=2,AD=3. 
(1)直接写出B、C、D三点的坐标;
(2)将矩形ABCD向右平移m个单位,使点A、C恰好同时落在反比例函数y= (x>0)的图象上,得矩形A'B'C'D'.求矩形ABCD的平移距离m和反比例函数的解析式.
(x>0)的图象上,得矩形A'B'C'D'.求矩形ABCD的平移距离m和反比例函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种“十位上的数字比个位、百位上的数字都要小”的三位数叫做“V数”如“947”就是一个“V数”.若十位上的数字为2,则从1,3,4,5中任选两数,能与2组成“V数”的概率是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.

(1)求证:AD平分∠BAC;
(2)若AC=8,tan∠DAC= ,求⊙O的半径.
,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠CAB=∠B=30°,AB=2
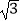 ,点D在BC边上,把△ABC沿AD翻折使AB与AC重合,得△AB′D,则△ABC与△AB′D重叠部分的面积为( )
,点D在BC边上,把△ABC沿AD翻折使AB与AC重合,得△AB′D,则△ABC与△AB′D重叠部分的面积为( ) 
A.
B.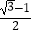
C.3﹣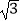
D.
相关试题

