【题目】某镇水库的可用水量为12000万立方米,假设年降水量不变,能维持该镇16万人20年的用水量.实施城市化建设,新迁入4万人后,水库只够维持居民15年的用水量.
(1)问:年降水量为多少万立方米?每人年平均用水量多少立方米?
(2)政府号召节约用水,希望将水库的保用年限提高到25年,则该镇居民人均每年需节约多少立方米才能实现目标?
参考答案:
【答案】
(1)解:设年降水量为x万立方米,每人每年平均用水量为y立方米,由题意,得
![]() ,
,
解得: ![]()
答:年降水量为200万立方米,每人年平均用水量为50立方米
(2)解:设该城镇居民年平均用水量为z立方米才能实现目标,由题意,得
12000+25×200=20×25z,
解得:z=34
则50﹣34=16(立方米).
答:该城镇居民人均每年需要节约16立方米的水才能实现目标
【解析】(1)设年降水量为x万立方米,每人每年平均用水量为y立方米,根据储水量+降水量=总用水量建立方程求出其解就可以了;(2)设该城镇居民年平均用水量为z立方米才能实现目标,同样由储水量+25年降水量=25年20万人的用水量为等量关系建立方程求出其解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校的校门是伸缩门(如图1),伸缩门中的每一行菱形有20个,每个菱形边长为30厘米.校门关闭时,每个菱形的锐角度数为60°(如图2);校门打开时,每个菱形的锐角度数从60°缩小为10°(如图3).问:校门打开了多少米?(结果精确到1米,参考数据:sin5°≈0.0872,cos5°≈0.9962,sin10°≈0.1736,cos10°≈0.9848).

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A、B的坐标分别是(0,3)、(﹣4,0),

(1)将△AOB绕点A逆时针旋转90°得到△AEF,点O,B对应点分别是E,F,请在图中画出△AEF,并写出E、F的坐标;
(2)以O点为位似中心,将△AEF作位似变换且缩小为原来的 ,在网格内画出一个符合条件的△A1E1F1 .
,在网格内画出一个符合条件的△A1E1F1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】小明在做课本“目标与评定”中的一道题:如图1,直线a,b所成的角跑到画板外面去了,你有什么办法量出这两条直线所成的角的度数?小明的做法是:如图2,画PC∥a,量出直线b与PC的夹角度数,即直线a,b所成角的度数.
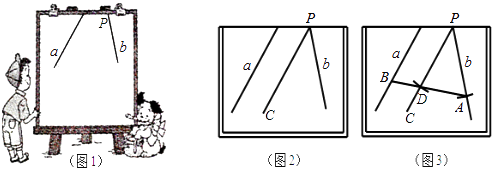
(1)请写出这种做法的理由;
(2)小明在此基础上又进行了如下操作和探究(如图3):①以P为圆心,任意长为半径画圆弧,分别交直线b,PC于点A,D;②连结AD并延长交直线a于点B,请写出图3中所有与∠PAB相等的角,并说明理由;
(3)请在图3画板内作出“直线a,b所成的跑到画板外面去的角”的平分线(画板内的部分),只要求作出图形,并保留作图痕迹. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线y=
 (x﹣m)2﹣
(x﹣m)2﹣  m2+m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.
m2+m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.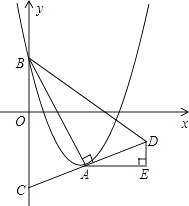
(1)当m=2时,求点B的坐标;
(2)求DE的长?
(3)①设点D的坐标为(x,y),求y关于x的函数关系式?②过点D作AB的平行线,与第(3)①题确定的函数图象的另一个交点为P,当m为何值时,以A,B,D,P为顶点的四边形是平行四边形? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(﹣
 ,3 ),AB=2,AD=3.
,3 ),AB=2,AD=3. 
(1)直接写出B、C、D三点的坐标;
(2)将矩形ABCD向右平移m个单位,使点A、C恰好同时落在反比例函数y= (x>0)的图象上,得矩形A'B'C'D'.求矩形ABCD的平移距离m和反比例函数的解析式.
(x>0)的图象上,得矩形A'B'C'D'.求矩形ABCD的平移距离m和反比例函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠C=90°,AC=BC.作射线AP,过点B作BD⊥AP于点D,连接CD.
(1)当射线AP位于图1所示的位置时
①根据题意补全图形;
②求证:AD+BD=
 CD.
CD.(2)当射线AP绕点A由图1的位置顺时针旋转至∠BAC的内部,如图2,直接写出此时AD,BD,CD三条线段之间的数量关系为 .

相关试题

