【题目】如图,在平面直角坐标系xOy中,抛物线y= ![]() (x﹣m)2﹣
(x﹣m)2﹣ ![]() m2+m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.
m2+m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.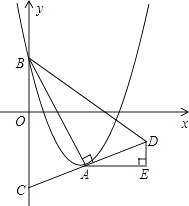
(1)当m=2时,求点B的坐标;
(2)求DE的长?
(3)①设点D的坐标为(x,y),求y关于x的函数关系式?②过点D作AB的平行线,与第(3)①题确定的函数图象的另一个交点为P,当m为何值时,以A,B,D,P为顶点的四边形是平行四边形?
参考答案:
【答案】
(1)
解:当m=2时,y= ![]() (x﹣2)2+1,
(x﹣2)2+1,
把x=0代入y= ![]() (x﹣2)2+1,得:y=2,
(x﹣2)2+1,得:y=2,
∴点B的坐标为(0,2)
(2)
解:延长EA,交y轴于点F,
∵AD=AC,∠AFC=∠AED=90°,∠CAF=∠DAE,
∴△AFC≌△AED,
∴AF=AE,
∵点A(m,﹣ ![]() m2+m),点B(0,m),
m2+m),点B(0,m),
∴AF=AE=|m|,BF=m﹣(﹣ ![]() m2+m)=
m2+m)= ![]() m2,
m2,
∵∠ABF=90°﹣∠BAF=∠DAE,∠AFB=∠DEA=90°,
∴△ABF∽△DAE,
∴ ![]() ,即:
,即: ![]() =
= ![]() ,
,
∴DE=4.
(3)
解:①∵点A的坐标为(m,﹣ ![]() m2+m),
m2+m),
∴点D的坐标为(2m,﹣ ![]() m2+m+4),
m2+m+4),
∴x=2m,y=﹣ ![]() m2+m+4,
m2+m+4,
∴y=﹣ ![]()
![]() +
+ ![]() +4,
+4,
∴所求函数的解析式为:y=﹣ ![]() x2+
x2+ ![]() x+4,
x+4,
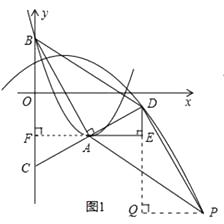
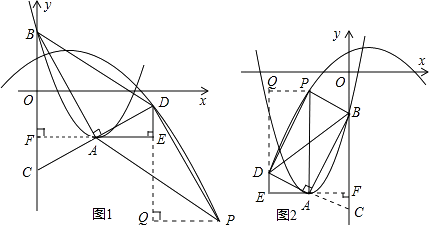
②作PQ⊥DE于点Q,则△DPQ≌△BAF,
(i)当四边形ABDP为平行四边形时(如图1),
点P的横坐标为3m,
点P的纵坐标为:(﹣ ![]() m2+m+4)﹣(
m2+m+4)﹣( ![]() m2)=﹣
m2)=﹣ ![]() m2+m+4,
m2+m+4,
把P(3m,﹣ ![]() m2+m+4)的坐标代入y=﹣
m2+m+4)的坐标代入y=﹣ ![]() x2+
x2+ ![]() x+4得:
x+4得:
﹣ ![]() m2+m+4=﹣
m2+m+4=﹣ ![]() ×(3m)2+
×(3m)2+ ![]() ×(3m)+4,
×(3m)+4,
解得:m=0(此时A,B,D,P在同一直线上,舍去)或m=8.
(ii)当四边形ABPD为平行四边形时(如图2),
点P的横坐标为m,
点P的纵坐标为:(﹣ ![]() m2+m+4)+(
m2+m+4)+( ![]() m2)=m+4,
m2)=m+4,
把P(m,m+4)的坐标代入y=﹣ ![]() x2+
x2+ ![]() x+4得:
x+4得:
m+4=﹣ ![]() m2+
m2+ ![]() m+4,
m+4,
解得:m=0(此时A,B,D,P在同一直线上,舍去)或m=﹣8,
综上所述:m的值为8或﹣8.
【解析】(1)将m=2代入原式,得到二次函数的顶点式,据此即可求出B点的坐标;(2)延长EA,交y轴于点F,证出△AFC≌△AED,进而证出△ABF∽△DAE,利用相似三角形的性质,求出DE=4;(3)①根据点A和点B的坐标,得到x=2m,y=﹣ ![]() m2+m+4,将m=
m2+m+4,将m= ![]() 代入y=﹣
代入y=﹣ ![]() m2+m+4,即可求出二次函数的表达式;
m2+m+4,即可求出二次函数的表达式;
②作PQ⊥DE于点Q,则△DPQ≌△BAF,然后分(如图1)和(图2)两种情况解答.
【考点精析】根据题目的已知条件,利用二次函数的性质的相关知识可以得到问题的答案,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A、B的坐标分别是(0,3)、(﹣4,0),

(1)将△AOB绕点A逆时针旋转90°得到△AEF,点O,B对应点分别是E,F,请在图中画出△AEF,并写出E、F的坐标;
(2)以O点为位似中心,将△AEF作位似变换且缩小为原来的 ,在网格内画出一个符合条件的△A1E1F1 .
,在网格内画出一个符合条件的△A1E1F1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】小明在做课本“目标与评定”中的一道题:如图1,直线a,b所成的角跑到画板外面去了,你有什么办法量出这两条直线所成的角的度数?小明的做法是:如图2,画PC∥a,量出直线b与PC的夹角度数,即直线a,b所成角的度数.
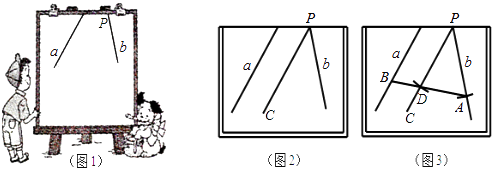
(1)请写出这种做法的理由;
(2)小明在此基础上又进行了如下操作和探究(如图3):①以P为圆心,任意长为半径画圆弧,分别交直线b,PC于点A,D;②连结AD并延长交直线a于点B,请写出图3中所有与∠PAB相等的角,并说明理由;
(3)请在图3画板内作出“直线a,b所成的跑到画板外面去的角”的平分线(画板内的部分),只要求作出图形,并保留作图痕迹. -
科目: 来源: 题型:
查看答案和解析>>【题目】某镇水库的可用水量为12000万立方米,假设年降水量不变,能维持该镇16万人20年的用水量.实施城市化建设,新迁入4万人后,水库只够维持居民15年的用水量.
(1)问:年降水量为多少万立方米?每人年平均用水量多少立方米?
(2)政府号召节约用水,希望将水库的保用年限提高到25年,则该镇居民人均每年需节约多少立方米才能实现目标? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(﹣
 ,3 ),AB=2,AD=3.
,3 ),AB=2,AD=3. 
(1)直接写出B、C、D三点的坐标;
(2)将矩形ABCD向右平移m个单位,使点A、C恰好同时落在反比例函数y= (x>0)的图象上,得矩形A'B'C'D'.求矩形ABCD的平移距离m和反比例函数的解析式.
(x>0)的图象上,得矩形A'B'C'D'.求矩形ABCD的平移距离m和反比例函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠C=90°,AC=BC.作射线AP,过点B作BD⊥AP于点D,连接CD.
(1)当射线AP位于图1所示的位置时
①根据题意补全图形;
②求证:AD+BD=
 CD.
CD.(2)当射线AP绕点A由图1的位置顺时针旋转至∠BAC的内部,如图2,直接写出此时AD,BD,CD三条线段之间的数量关系为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种“十位上的数字比个位、百位上的数字都要小”的三位数叫做“V数”如“947”就是一个“V数”.若十位上的数字为2,则从1,3,4,5中任选两数,能与2组成“V数”的概率是( )
A.
B.
C.
D.
相关试题

