【题目】如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(﹣ ![]() ,3 ),AB=2,AD=3.
,3 ),AB=2,AD=3. 
(1)直接写出B、C、D三点的坐标;
(2)将矩形ABCD向右平移m个单位,使点A、C恰好同时落在反比例函数y= ![]() (x>0)的图象上,得矩形A'B'C'D'.求矩形ABCD的平移距离m和反比例函数的解析式.
(x>0)的图象上,得矩形A'B'C'D'.求矩形ABCD的平移距离m和反比例函数的解析式.
参考答案:
【答案】
(1)解:∵四边形ABCD是矩形,
∴AB=CD=2,BC=AD=3,
∵A(﹣ ![]() ,3 ),AD∥x轴,
,3 ),AD∥x轴,
∴B(﹣ ![]() ,1),C(﹣
,1),C(﹣ ![]() ,1),D(﹣
,1),D(﹣ ![]() ,3)
,3)
(2)解:∵将矩形ABCD向右平移m个单位,
∴A′(﹣ ![]() +m,3),C(﹣
+m,3),C(﹣ ![]() +m,1),
+m,1),
∵点A′,C′在反比例函数y= ![]() (x>0)的图象上,
(x>0)的图象上,
∴3×(﹣ ![]() +m)=1×(﹣
+m)=1×(﹣ ![]() +m),
+m),
解得:m=6,
∴B′( ![]() ,1),
,1),
∴k= ![]() ×1=
×1= ![]() ,
,
∴矩形ABCD的平移距离m=6,
反比例函数的解析式为:y= ![]()
【解析】(1)由四边形ABCD是矩形,得到AB=CD=2,BC=AD=3,根据A(﹣ ![]() ,3 ),AD∥x轴,即可得到B(﹣
,3 ),AD∥x轴,即可得到B(﹣ ![]() ,1),C(﹣
,1),C(﹣ ![]() ,1),D(﹣
,1),D(﹣ ![]() ,3);(2)根据平移的性质将矩形ABCD向右平移m个单位,得到A′(﹣
,3);(2)根据平移的性质将矩形ABCD向右平移m个单位,得到A′(﹣ ![]() +m,3),C(﹣
+m,3),C(﹣ ![]() +m,1),由点A′,C′在反比例函数y=
+m,1),由点A′,C′在反比例函数y= ![]() (x>0)的图象上,得到方程 3×(﹣
(x>0)的图象上,得到方程 3×(﹣ ![]() +m)=1×(﹣
+m)=1×(﹣ ![]() +m),即可求得结果.
+m),即可求得结果.
【考点精析】掌握矩形的性质是解答本题的根本,需要知道矩形的四个角都是直角,矩形的对角线相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在做课本“目标与评定”中的一道题:如图1,直线a,b所成的角跑到画板外面去了,你有什么办法量出这两条直线所成的角的度数?小明的做法是:如图2,画PC∥a,量出直线b与PC的夹角度数,即直线a,b所成角的度数.
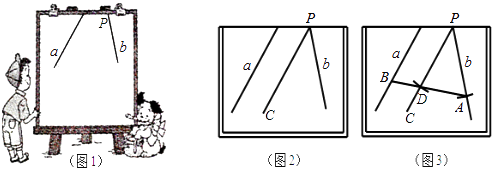
(1)请写出这种做法的理由;
(2)小明在此基础上又进行了如下操作和探究(如图3):①以P为圆心,任意长为半径画圆弧,分别交直线b,PC于点A,D;②连结AD并延长交直线a于点B,请写出图3中所有与∠PAB相等的角,并说明理由;
(3)请在图3画板内作出“直线a,b所成的跑到画板外面去的角”的平分线(画板内的部分),只要求作出图形,并保留作图痕迹. -
科目: 来源: 题型:
查看答案和解析>>【题目】某镇水库的可用水量为12000万立方米,假设年降水量不变,能维持该镇16万人20年的用水量.实施城市化建设,新迁入4万人后,水库只够维持居民15年的用水量.
(1)问:年降水量为多少万立方米?每人年平均用水量多少立方米?
(2)政府号召节约用水,希望将水库的保用年限提高到25年,则该镇居民人均每年需节约多少立方米才能实现目标? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线y=
 (x﹣m)2﹣
(x﹣m)2﹣  m2+m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.
m2+m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.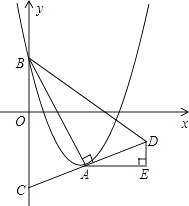
(1)当m=2时,求点B的坐标;
(2)求DE的长?
(3)①设点D的坐标为(x,y),求y关于x的函数关系式?②过点D作AB的平行线,与第(3)①题确定的函数图象的另一个交点为P,当m为何值时,以A,B,D,P为顶点的四边形是平行四边形? -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠C=90°,AC=BC.作射线AP,过点B作BD⊥AP于点D,连接CD.
(1)当射线AP位于图1所示的位置时
①根据题意补全图形;
②求证:AD+BD=
 CD.
CD.(2)当射线AP绕点A由图1的位置顺时针旋转至∠BAC的内部,如图2,直接写出此时AD,BD,CD三条线段之间的数量关系为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种“十位上的数字比个位、百位上的数字都要小”的三位数叫做“V数”如“947”就是一个“V数”.若十位上的数字为2,则从1,3,4,5中任选两数,能与2组成“V数”的概率是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.

(1)求证:AD平分∠BAC;
(2)若AC=8,tan∠DAC= ,求⊙O的半径.
,求⊙O的半径.
相关试题

