【题目】如图,在平面直角坐标系中,直线AB与y轴交于点A,与x轴交于点B,且∠BAO=30°,现将△OAB沿直线AB翻折,得到△CAB. 连接OC交AB于点D.
(1)求证:AD⊥OC,OD=![]() OA ;
OA ;
(2)若Rt△AOB的斜边AB=![]() ,则OB=_____;OA=_____;点C的坐标为_______;
,则OB=_____;OA=_____;点C的坐标为_______;
(3)在(2)的条件下,动点F从点O出发,以2个单位长度/秒的速度沿折线O﹣A﹣C向终点C运动,设△FOB的面积为S(S>0),点F的运动时间为t秒,求S与t的关系式,并直接写出t的取值范围;
(4)在(3)的条件下,过点B作BE⊥x轴,交AC于点E,在动点F的运动过程中,当t为何值时,△BEF是以BE为腰的等腰三角形?

参考答案:
【答案】 (1)见解析; (2)![]() ,6, (
,6, (![]() ,3) (3)
,3) (3) 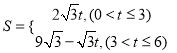 ;(4) 当t=1或3时,△BEF是以BE为腰的等腰三角形.
;(4) 当t=1或3时,△BEF是以BE为腰的等腰三角形.
【解析】试题分析:(1)根据折叠的性质和等边三角形的判定得到△OAC是等边三角形;结合等边三角形的“三线合一”的性质证得结论;
(2)如图1,过C点作CH⊥x轴于H点,在直角△OCH中,利用三角函数求得CH和OH,则C的坐标即可求得;
(3)分成当0<t≤3和3<t≤6两种情况,利用三角形的面积公式即可求解;
(4)分成B是顶角顶点和E是顶角顶点两种情况进行讨论.
试题解析:
(1)由折叠得性质得: CA=OA, CB=OB,∠BAC=∠BAO=30°,∠ACB=∠AOB=90°,
∴ ∠ABC=∠ABO=60°,
∴ △OAC是等边三角形
∴OC=OA ,
∵ ∠DAC=∠DAO ,
∴ AD⊥OC且OD=![]() OC ;
OC ;
∴ AD⊥OC且OD=![]() OA ;
OA ;
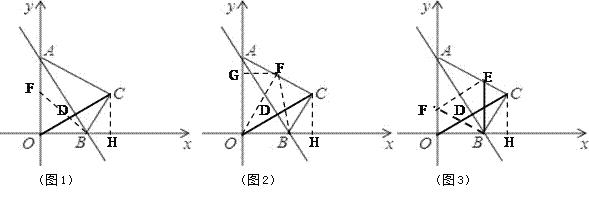
(2) OB=![]() ; OA=6; C(
; OA=6; C(![]() ,3);
,3);
(3)分两种情况讨论:
①当0<t≤3时,如图1, OF=2t, ![]() ;
;
②当3<t≤6时,如图2, AF=2t﹣6, 过点F作FG⊥OA于G,
则 ![]() , OG=OA- AG=6﹣(t﹣3)=9﹣t,
, OG=OA- AG=6﹣(t﹣3)=9﹣t,
![]() ;
;
综上所述: 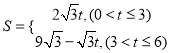
(4)分两种情况讨论:
① 当腰BE=BF时, 如图3,
∵BE∥OA ,
∴∠ABE=∠OAB=30° ,
∴∠EBA=∠EAB=30° ,
∴BE=AE 且∠EBC=60°-30°=30° ,
∵在Rt△BOF和Rt△BCE中,BF=BE ,BO=BC ,
∴△BOF≌△BCE,(HL)
∴OF=CE 且 ∠FBO=∠EBC=30° ,
∴∠EBF=120°-30°-30°60° ,
∴ 此时△BEF为等边三角形.BF=AF,
在Rt△FBO 中,∵ ∠FBO=30°
∴ FO=![]() BF=
BF=![]() AF,
AF,
∴AF=2 FO.
∴AO=3FO.
∴3FO=6,
∴ FO=2 ,
∴ 2t=2,
∴此时t=1,
②当腰BE=FE时,由上可知,点F使得△BEF为等边三角形 或 点F运动与A点重合,
则 2t=2,或者 2t=6,
∴ 此时 t=1,或 t=3,;
综上所述,当t=1或3时,△BEF是以BE为腰的等腰三角形.
-
科目: 来源: 题型:
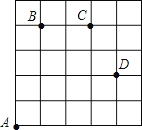
查看答案和解析>>【题目】如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(﹣1,﹣4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
(1)A→C( , ),B→D( , );
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(3)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+1,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出依次行走停点E、F、M、N的位置.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方形OABC的顶点为O(0,0),A(1,0),B(1,1),C(0,1).
(1)判断直线
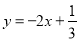 与正方形OABC是否有交点,并求交点坐标。
与正方形OABC是否有交点,并求交点坐标。(2)将直线
 进行平移,平移后恰好能把正方形OABC分为面积相等的两部分,请求出平移后的直线解析式.
进行平移,平移后恰好能把正方形OABC分为面积相等的两部分,请求出平移后的直线解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2x+9≥3(x+2)的正整数解是
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果二次函数y=(m-2)x2+3x+m2-4的图像经过原点,则m的值为( )
A. 2B. ±2C. -2D. 0或2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y与x-3成正比例,当x=4时,y=3.
(1) 求出y与x之间的函数关系式;
(2) y与x之间是什么函数关系? 并在平面直角坐标系中画出该函数的图像;
(3) 当x=2.5时,y的值为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
第1个等式:
 ;
;第2个等式:
 ;
;第3个等式:
 ;
;第4个等式:
 );
);…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= = ;
(2)用含有n的代数式表示第n个等式:an= = (n为正整数);
(3)求a1+a2+a3+a4+…+a100的值.
相关试题

