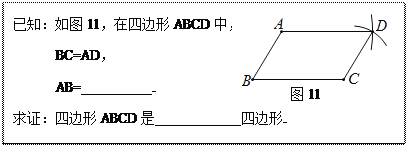
【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图11的四边形ABCD,并写出了如下不完整的已知和求证。

(1)在方框中填空,以补全已知和求证;
(2)按嘉淇同学的想法写出证明;
证明:
(3)用文字叙述所证命题的逆命题为
参考答案:
【答案】(1)已知、求证见解析;(2)证明见解析;(3)平行四边形两组对边分别相等.
【解析】试题分析:(1)命题的题设为“两组对边分别相等的四边形”,结论是“是平行四边形”,根据题设可得已知:在四边形ABCD中,BC=AD,AB=CD,求证:四边形ABCD是平行四边形;
(2)连接BD,利用SSS定理证明△ABD≌△CDB,得到∠ADB=∠DBC,∠ABD=∠CDB,进而得到AB∥CD,AD∥CB,即可得到结论;
(3)把命题“两组对边分别相等的四边形是平行四边形”的题设和结论对换可得平行四边形两组对边分别相等.
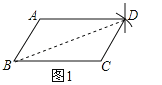
(1)已知:如图1,在四边形ABCD中,BC=AD,AB=CD,
求证:四边形ABCD是平行四边形.故答案为:CD,平行;
(2)连接BD,在△ABD和△CDB中,∵AB=CD,AD=BC,BD=DB,∴△ABD≌△CDB(SSS),∴∠ADB=∠DBC,∠ABD=∠CDB,∴AB∥CD,AD∥CB,∴四边形ABCD是平行四边形;
(3)用文字叙述所证命题的逆命题为:平行四边形两组对边分别相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD是正方形(提示:正方形四边相等,四个角都是90°)

(1)如图1,点G是BC边上任意一点(不与点B、C重合),连接AG,作BF⊥AG于点F,DE⊥AG于点E.
求证:△ABF≌△DAE;
(2)直接写出(1)中,线段EF与AF、BF的等量关系 ;
(3)①如图2,若点G是CD边上任意一点(不与点C、D重合),连接AG,作BF⊥AG于点F,DE⊥AG于点E,则图中全等三角形是 ,线段EF与AF、BF的等量关系是 ;
②如图3,若点G是CD延长线上任意一点,连接AG,作BF⊥AG于点F,DE⊥AG于点E,线段EF与AF、BF的等量关系是 ;
(4)若点G是BC延长线上任意一点,连接AG,作BF⊥AG于点F,DE⊥AG于点E,请画图、探究线段EF与AF、BF的等量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是⊙O的内接三角形,AE是⊙O的直径,AF是⊙O的弦,AF⊥BC,垂足为D.
(1)求证:∠BAE=∠CAD.
(2)若⊙O的半径为4,AC=5,CD=2,求CF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对于下列各值:①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;其中会随点P的移动而变化的是( )

A. ① B. ② C. ③ D. ④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学生数学的平时成绩、期中考试成绩、期末考试成绩分别是84分、80分、90分。如果按平时成绩:期中考试成绩:期末考试成绩=3:3:4进行总评,那么他本学期数学总评分应为______分。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂生产A,B两种产品,其单价随市场变化而做相应调整,营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图:

并求得了A产品三次单价的平均数和方差:
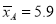 ;
; 
(1)补全图中B产品单价变化的折线图,B产品第三次的单价比上一次的单价降低了 %;
(2)求B产品三次单价的平均数和方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,若B产品第四次调价后为m元(3<m<4),此时B产品四次单价的中位数是A产品这四次单价的中位数的
 倍,求m.
倍,求m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式由左边到右边的变形中,属于因式分解的是( )
A.(a﹣2)(a+2)=a2﹣4
B.8x2y=8×x2y
C.m2﹣1+n2=(m+1)(m﹣1)+n2
D.x2+2x﹣3=(x﹣1)(x+3)
相关试题

