【题目】如图,△ABC是⊙O的内接三角形,AE是⊙O的直径,AF是⊙O的弦,AF⊥BC,垂足为D.
(1)求证:∠BAE=∠CAD.
(2)若⊙O的半径为4,AC=5,CD=2,求CF.

参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)由圆周角定理得出∠ABE=90°,得出∠BAE+∠BEA=90°,由AF⊥BC得出∠ACD+∠CAD=90°,由圆周角定理得出∠BEA=∠ACD,即可得出结论;(2)证明△ABE∽△ADC,得出对应边成比例![]() ,求出BE,由圆周角定理
,求出BE,由圆周角定理![]() ,得出CF=BE=
,得出CF=BE=![]() 即可.
即可.
试题解析:(1)证明:∵AE是O的直径,
∴∠ABE=90°,
∴∠BAE+∠BEA=90°,
∵AF⊥BC,
∴∠ADC=90°,
∴∠ACD+∠CAD=90°,
又∵∠BEA=∠ACD,
∴∠BAE=∠CAD;
(2)∵∠ABE=∠ADC=90°,∠BEA=∠ACD,
∴△ABE∽△ADC,
∴![]() ,即
,即![]() ,
,
解得:BE=![]() ,
,
由(1)得:∠BAE=∠CAD,
∴![]() ,
,
∴CF=BE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某研究所将某种材料加热到1000℃时停止加热,并立即将材料分为A、B两组,采用不同工艺做降温对比实验,设降温开始后经过x min时,A、B两组材料的温度分别为yA℃、yB℃,yA、yB与x的函数关系式分别为yA=kx+b,yB=
 (x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.
(x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.
(1)分别求yA、yB关于x的函数关系式;
(2)当A组材料的温度降至120℃时,B组材料的温度是多少?
(3)在0<x<40的什么时刻,两组材料温差最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD是正方形(提示:正方形四边相等,四个角都是90°)

(1)如图1,点G是BC边上任意一点(不与点B、C重合),连接AG,作BF⊥AG于点F,DE⊥AG于点E.
求证:△ABF≌△DAE;
(2)直接写出(1)中,线段EF与AF、BF的等量关系 ;
(3)①如图2,若点G是CD边上任意一点(不与点C、D重合),连接AG,作BF⊥AG于点F,DE⊥AG于点E,则图中全等三角形是 ,线段EF与AF、BF的等量关系是 ;
②如图3,若点G是CD延长线上任意一点,连接AG,作BF⊥AG于点F,DE⊥AG于点E,线段EF与AF、BF的等量关系是 ;
(4)若点G是BC延长线上任意一点,连接AG,作BF⊥AG于点F,DE⊥AG于点E,请画图、探究线段EF与AF、BF的等量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对于下列各值:①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;其中会随点P的移动而变化的是( )

A. ① B. ② C. ③ D. ④
-
科目: 来源: 题型:
查看答案和解析>>【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图11的四边形ABCD,并写出了如下不完整的已知和求证。
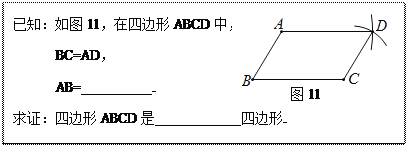

(1)在方框中填空,以补全已知和求证;
(2)按嘉淇同学的想法写出证明;
证明:
(3)用文字叙述所证命题的逆命题为
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学生数学的平时成绩、期中考试成绩、期末考试成绩分别是84分、80分、90分。如果按平时成绩:期中考试成绩:期末考试成绩=3:3:4进行总评,那么他本学期数学总评分应为______分。
相关试题

