【题目】如图,在四边形ABCD中,AD∥BC,F在CD上,且AF垂直平分CD,FG平分∠AFD,交AD于G,连接GB,交AF于N,且FN=FD.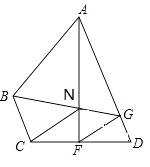
(1)求证:△GFN≌△GFD;
(2)如图,连接ND,若BC=ND,∠ADC=75°,求证:AN=AB;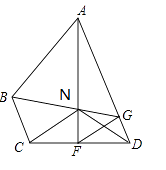
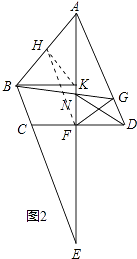
(3)如图2,延长AF、BC交于点E,过B作BK⊥AE于K,若∠BAF=2∠E,猜想,AB与KF之间有何数量关系?请说明理由.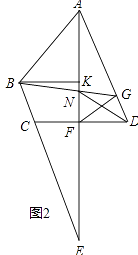
参考答案:
【答案】
(1)
证明:∵FG平分∠AFD,
∴∠NFG=∠GFD,
在△GFN和△GFD中, 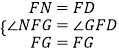 ,
,
∴△GFN≌△GFD(SAS)
(2)
证明:连接AC,如图1所示:
∵AF⊥CD,FN=FD,
∴△DFN为等腰直角三角形,
∴∠FDN=45°,
∵∠ADC=75°,
∴∠ADN=∠ADC﹣∠FDN=75°﹣45°=30°,
在Rt△AFD中,∠FAD=90°﹣75°=15°
∵AF垂直平分CD,
∴AC=AD,
∴∠ACD=∠ADC=75°,
∴∠CAD=30°,
∵AD∥BC,
∴∠BCA=∠CAD=30°,
∴∠ADN=∠BCA,
在△ADN和△ACB中, 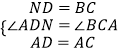 ,
,
∴△ADN≌△ACB(SAS),
∴AN=AB
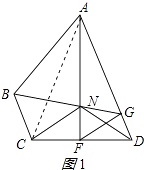
(3)
解:AB与KF之间有何数量关系为:AB=2KF;理由如下:
取AB中点H,连接HF、HK,如图2所示:
∵在Rt△AKB中,H为AB中点,
∴HK= ![]() AB=AH,
AB=AH,
∴∠HAK=∠HKA,
∵∠BAF=2∠E,
∴∠HKA=2∠E,
∵AD∥BE,
∴△AFD∽△EFC,
∴ ![]() =
= ![]() =1,
=1,
∴AF=EF,
∵H为AB中点,
∴HF为△ABE的中位线,
∴HF∥BE,
∴∠HFK=∠E,
∴∠HKA=2∠HFK,
∵∠HKA=∠HFK+∠FHK,
∴2∠HFK=∠HFK+∠FHK,
∴∠HFK=∠FHK,
∴HK=KF,
∵HK= ![]() AB,
AB,
即AB=2HK,
∴AB=2KF.
【解析】(1)由角平分线得出∠NFG=∠GFD,由SAS证明△GFN≌△GFD即可;(2)连接AC,由等腰直角三角形的性质得出∠FDN=45°,由线段垂直平分线的性质得出AC=AD,证出∠CAD=30°,由SAS证明△ADN≌△ACB,得出对应边相等即可;(3)取AB中点H,连接HF、HK,由直角三角形斜边上的中线性质得出HK= ![]() AB=AH,得出∠HAK=∠HKA,证明△AFD∽△EFC,得出对应边成比例,证出AF=EF,证明HF为△ABE的中位线,由三角形中位线定理得出HF∥BE,得出∠HFK=∠E,由角的关系得出∠HFK=∠FHK,得出HK=KF,即可得出结论.
AB=AH,得出∠HAK=∠HKA,证明△AFD∽△EFC,得出对应边成比例,证出AF=EF,证明HF为△ABE的中位线,由三角形中位线定理得出HF∥BE,得出∠HFK=∠E,由角的关系得出∠HFK=∠FHK,得出HK=KF,即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数a,b满足(2a+1)2+|a+b+1|=0,且关于x,y的方程组
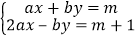 的解x<0,y>0,求m的取值范围.
的解x<0,y>0,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】将两个底边相等的等腰三角形按照图所示的方式拼接在一起(隐藏互相重合的底边)的图形俗称为“筝形”.假如“筝形”下个定义,那么下面四种说法中,你认为最能够描述“筝形”特征的是 ( )
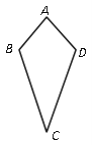
A. 有两组邻边相等的四边形称为“筝形”;
B. 有两组对角分别相等的四边形称为“筝形”;
C. 两条对角线互相垂直的四边形称为“筝形”;
D. 以一条对角线所在直线为对称轴的四边形称为“筝形”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式﹣4x≥﹣12的正整数解为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:对于实数a,符号[a]表示不大于a的最大整数,例如:[4.7]=4,[﹣π]=﹣4,[3]=3,如果[
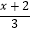 +1]=﹣5,则x的取值范围为 .
+1]=﹣5,则x的取值范围为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,由下列条件不能判定△ABC为直角三角形的是( )
A. ∠A+∠B=∠C B. ∠A:∠B:∠C=1:2:3
C. a2=c2﹣b2 D. a:b:c=3:4:6
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人共同解方程组
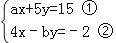 , 由于甲错了方程①中的a,得到方程组的解为
, 由于甲错了方程①中的a,得到方程组的解为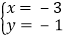 ;乙看错了方程②中的b,得到方程组的解为
;乙看错了方程②中的b,得到方程组的解为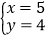 ,
,
(1)求出a,b的值;
(2)求2a﹣3b+5的立方根;
(3)此方程组正确的解应该是多少?
相关试题

