【题目】已知实数a,b满足(2a+1)2+|a+b+1|=0,且关于x,y的方程组![]() 的解x<0,y>0,求m的取值范围.
的解x<0,y>0,求m的取值范围.
参考答案:
【答案】解:∵(2a+1)2+|a+b+1|=0,
∴2a+1=0,a+b+1=0,
解得:a=![]() , b=
, b=![]() ,
,
代入方程组![]() 得:
得: ,
,
解得:x=![]() , y=
, y=![]() ,
,
, ∵x<0,y>0,
∴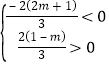 ,
,
解不等式组得:![]() <m<1,
<m<1,
即m的取值范围是:![]() <m<1.
<m<1.
【解析】根据偶次方,绝对值得出2a+1=0,a+b+1=0,求出a、b的值,代入方程组得出关于x、y的方程组,求出法则的解,根据x<0,y>0得出关于m的不等式组,求出不等式组的解集即可.
【考点精析】根据题目的已知条件,利用二元一次方程的解和一元一次不等式组的解法的相关知识可以得到问题的答案,需要掌握适合一个二元一次方程的一组未知数的值,叫做这个二元一次方程的一个解;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
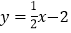 与x轴交于点B,与y轴交于点C,抛物线
与x轴交于点B,与y轴交于点C,抛物线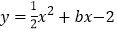
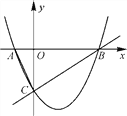
与x轴交于A、B两点(A在B的左侧),与y轴交于点C.
(1)求抛物线的解析式;
(2)点M是上述抛物线上一点,如果△ABM和△ABC相似,求点M的坐标;
(3)连接AC,求顶点D、E、F、G在△ABC各边上的矩形DEFC面积最大时,写出该矩形在AB边上的顶点的坐标.
-
科目: 来源: 题型:
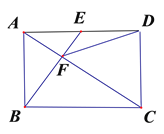
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,
(1)求证:CF=2AF;
(2)求tan∠CFD的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】8月25日,高德公司发布了《2015年第二季度中国主要城市交通分析报告》,在国内城市拥堵排行中,北京、杭州、广州位列前三,山城重庆排第九.为了解重庆市交通拥堵情况,经调查统计:菜园坝长江大桥上的车流速度V(单位:千米/时)是车流密度x(单位:辆/千米)的一次函数,且满足v=﹣
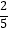 x+88(其中20≤x≤220).
x+88(其中20≤x≤220).
(1)在交通高峰时段,为使菜园坝长江大桥上车流速度不小于48千米/时且不大于60千米/时,应控制
菜园坝长江大桥上的车流密度在什么范围内?
(2)若规定车流量(单位:辆/时)是单位时间内通过桥上某观测点的车辆数.即:车流量=车流速度×车
流密度.那在(1)的条件下.菜园坝长江大桥上车流量的最大值是多少?
(3)当车流量为4680辆/时时,为了使桥上的更畅通,则桥上的车流密度应为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】将两个底边相等的等腰三角形按照图所示的方式拼接在一起(隐藏互相重合的底边)的图形俗称为“筝形”.假如“筝形”下个定义,那么下面四种说法中,你认为最能够描述“筝形”特征的是 ( )
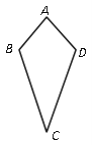
A. 有两组邻边相等的四边形称为“筝形”;
B. 有两组对角分别相等的四边形称为“筝形”;
C. 两条对角线互相垂直的四边形称为“筝形”;
D. 以一条对角线所在直线为对称轴的四边形称为“筝形”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式﹣4x≥﹣12的正整数解为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,F在CD上,且AF垂直平分CD,FG平分∠AFD,交AD于G,连接GB,交AF于N,且FN=FD.
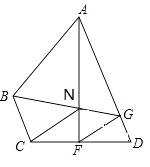
(1)求证:△GFN≌△GFD;
(2)如图,连接ND,若BC=ND,∠ADC=75°,求证:AN=AB;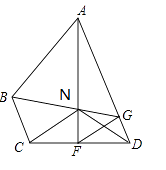
(3)如图2,延长AF、BC交于点E,过B作BK⊥AE于K,若∠BAF=2∠E,猜想,AB与KF之间有何数量关系?请说明理由.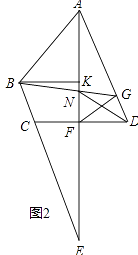
相关试题

