【题目】如图,△ABC为等边三角形,∠BAD=∠ACF=∠CBE,求∠DEC的度数。

参考答案:
【答案】120°
【解析】试题分析:根据等边三角形的性质和已知条件易证△ACF≌△CBE≌△BAD,再由等边三角形的性质和等边三角形的判定方法易证△DEF为等边三角形,可得∠DEF =60°,根据平角的定义即可求得∠DEC的度数.
试题解析:
∵△ABC为等边三角形,
∴AB=AC=BC,∠BAC=∠ABC=∠ACB;
又∵∠BAD=∠CBE=∠ACF,
∴∠BAC-∠BAD=∠ABC-∠CBE=∠ACB-∠ACF,
∴∠CAF=∠ABE=∠BCE,
∴△ACF≌△CBE≌△BAD(ASA).
∴AF=BD=CE,AD=BE=CF,
∴AD-AF=BE-BD=CF-CE,
∴DF=DE=EF,
∴△DEF为等边三角形,
∴∠DEF=∠DFE=∠EDF=60°,
又 点C点F点E三点共线,
∴∠DEC=120°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲组有10人,乙组有14人.现在另增调12人加入到甲组或乙组,要使乙组人数是甲组人数的2倍,则甲组应调来_____人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数1,1,2,3,5,8,13是“斐波那契数列”的一部分,若去掉其中的两个数后这组数的中位数、众数保持不变,则去掉的两个数是( )
A.2,5B.1,2C.2,3D.5,8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=30°,点M,N分别是射线OA,OB上的动点,OP平分∠AOB,且OP=6,△PMN的周长最小值为________.
-
科目: 来源: 题型:
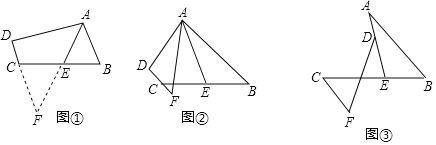
查看答案和解析>>【题目】(1)阅读理解:如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.
AB、AD、DC之间的等量关系为 ;
(2)问题探究:如图②,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
(3)问题解决:如图③,AB∥CF,AE与BC交于点E,BE:EC=2:3,点D在线段AE上,且∠EDF=∠BAE,试判断AB、DF、CF之间的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知A(1,-5),B(4,2),C(-1,0)三点.
(1)点B关于x轴对称点B′的坐标为 ,点C关于y轴对称点C′的坐标为 ;
(2)求(1)中的△AB′C′的面积.
-
科目: 来源: 题型:
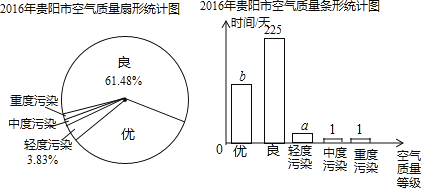
查看答案和解析>>【题目】2017年6月2日,贵阳市生态委发布了《2016年贵阳市环境状况公报》,公报显示,2016年贵阳市生态环境质量进一步提升,小颖根据公报中的部分数据,制成了下面两幅统计图,请根据图中提供的信息,回答下列问题:
(1)a= ,b= ;(结果保留整数)
(2)求空气质量等级为“优”在扇形统计图中所占的圆心角的度数;(结果精确到1°)
(3)根据了解,今年1~5月贵阳市空气质量优良天数为142天,优良率为94%,与2016年全年的优良率相比,今年前五个月贵阳市空气质量的优良率是提高还是降低了?请对改善贵阳市空气质量提一条合理化建议.
相关试题

