【题目】一组数1,1,2,3,5,8,13是“斐波那契数列”的一部分,若去掉其中的两个数后这组数的中位数、众数保持不变,则去掉的两个数是( )
A.2,5B.1,2C.2,3D.5,8
参考答案:
【答案】A
【解析】
根据中位数和众数的定义确定原来中位数和众数分别是多少,然后即可确定答案.
1,1,2,3,5,8,13的众数为1,中位数为3,
所以应该以3为中心左右对称去,且不能去掉1,
所以去掉2,5后中位数仍为3,众数仍为1.
故选:A.
-
科目: 来源: 题型:
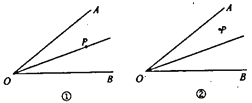
查看答案和解析>>【题目】如图①,OP是∠AOB的平分线。请过点P画一条直线,在∠AOB上截得一个等腰三角形,又如图②,如果点P是任命的一点,那么能否过这一点画一条直线,也在∠AOB上截得一个等腰三角形呢?请你画一画。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求∠A,∠ADB的度数。

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲组有10人,乙组有14人.现在另增调12人加入到甲组或乙组,要使乙组人数是甲组人数的2倍,则甲组应调来_____人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=30°,点M,N分别是射线OA,OB上的动点,OP平分∠AOB,且OP=6,△PMN的周长最小值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,∠BAD=∠ACF=∠CBE,求∠DEC的度数。

-
科目: 来源: 题型:
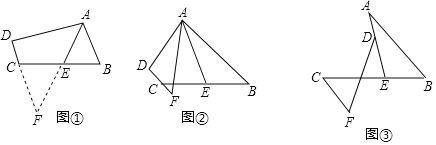
查看答案和解析>>【题目】(1)阅读理解:如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.
AB、AD、DC之间的等量关系为 ;
(2)问题探究:如图②,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
(3)问题解决:如图③,AB∥CF,AE与BC交于点E,BE:EC=2:3,点D在线段AE上,且∠EDF=∠BAE,试判断AB、DF、CF之间的数量关系,并证明你的结论.
相关试题

