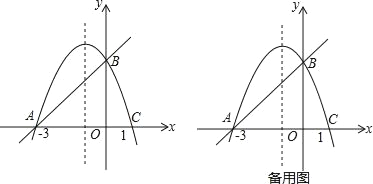
【题目】如图,在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c经过A、B、C三点,已知点A(﹣3,0),B(0,m),C(1,0).
(1)求m值;
(2)设点P是直线AB上方的抛物线上一动点(不与点A、B重合).
①过点P作x轴的垂线,垂足为F,交直线AB于点E,作PD⊥AB于点D.动点P在什么位置时,△PDE的周长最大,求出此时P点的坐标;
②连接AP,并以AP为边作等腰直角△APQ,当顶点Q恰好落在抛物线的对称轴上时,求出对应的点P坐标.
参考答案:
【答案】(1)m的值为3;(2)①点P坐标为(﹣![]() ,
,![]() );②点P的坐标为(
);②点P的坐标为(![]() )、(﹣1﹣
)、(﹣1﹣![]() ,2)、(﹣2,3)
,2)、(﹣2,3)
【解析】
(1)只需把点A、C的坐标代入y=﹣x2+bx+c,就可求出抛物线的解析式,就可求出m的值.
(2)①易得△PDE是等腰直角三角形,PE最大时△PDE的周长就最大.用待定系数法求出直线AB的解析式,设点P的横坐标为a,则点E的横坐标也为a,则点P、E的纵坐标就可用a的代数式表示,PE的长度也就可以用a的代数式表示,然后运用二次函数的最值性就可求出PE最大(即△PDE的周长最大)时,点P的坐标.
②等腰直角△APQ的三边都可能是底边,故分三种情况进行讨论,然后构造全等三角形,得到相等线段,然后用一个字母表示一条线段,从而将点P的坐标用该字母表示,然后代入抛物线的解析式,就可求出点P的坐标.
(1)∵抛物线y=﹣x2+bx+c经过点A(﹣3,0),C(1,0),∴![]() .
.
解得:![]() ,∴抛物线的解析式为y=﹣x2﹣2x+3.
,∴抛物线的解析式为y=﹣x2﹣2x+3.
∵点B(0,m)在抛物线y=﹣x2﹣2x+3上,∴m=3,∴m的值为3.
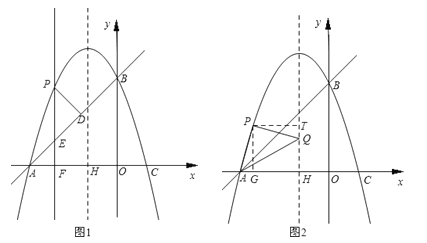
(2)①如图1.
∵OA=OB=3,∠AOB=90°,∴∠AB0=45°.
∵PF⊥OA,PD⊥AB,∴∠PDA=∠EFA=90°=∠AOB,∴EF∥OB,∴∠PED=∠ABO=45°,∴PD=PEsin45°![]() PE,DE=PEcos45°
PE,DE=PEcos45°![]() PE,∴△PDE的周长为(
PE,∴△PDE的周长为(![]() 1)PE.
1)PE.
设直线AB的解析式为y=mx+n,则有![]() .
.
解得:![]() ,∴直线AB的解析式为y=x+3.
,∴直线AB的解析式为y=x+3.
设点P的横坐标为a,则点E的横坐标也为a,∴yP=﹣a2﹣2a+3,yE=a+3,∴PE=yP﹣yE=(﹣a2﹣2a+3)﹣(a+3)=﹣a2﹣3a=﹣(a![]() )2
)2![]() .
.
∵﹣1<0,∴当a![]() 时,PE取到最大值,△PDE的周长也就取到最大值.
时,PE取到最大值,△PDE的周长也就取到最大值.
此时yP=﹣(![]() )2﹣2×(
)2﹣2×(![]() )+3
)+3![]() ,∴当点P坐标为(
,∴当点P坐标为(![]() )时,△PDE的周长取到最大值.
)时,△PDE的周长取到最大值.
②Ⅰ.若AQ为等腰直角△APQ的底边,如图2,则有AP=PQ,∠APQ=90°.
过点P作PG⊥OA,垂足为G,过点P作PT⊥QH,垂足为T.
∵∠PGH=∠GHT=PTH=90°,∴四边形PGHT是矩形,∴∠GPT=90°,PT=GH,PG=HT,∴∠APG=90°﹣∠GPQ=∠TPQ.
在△AGP和△QTP中,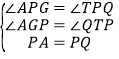 ,∴△AGP≌△QTP,∴AG=TQ,PG=PT,∴PG=GH.
,∴△AGP≌△QTP,∴AG=TQ,PG=PT,∴PG=GH.
∵抛物线y=﹣x2﹣2x+3的对称轴为x![]() 1,∴OH=1.
1,∴OH=1.
设PG=t(t>0),则OG=GH+OH=PG+OH=t+1.
∵点P在第二象限,∴点P的坐标为(﹣t﹣1,t).
∵点P在抛物线y=﹣x2﹣2x+3上,∴t=﹣(﹣t﹣1)2﹣2(﹣t﹣1)+3.
整理得:t2+t﹣4=0.
解得:t1![]() (舍去),t2
(舍去),t2![]() ,∴点P的坐标为(
,∴点P的坐标为(![]() ).
).
Ⅱ.若PQ为等腰直角△APQ的底边,如图3,则有AP=AQ,∠PAQ=90°.
过点P作PG⊥OA,垂足为G,则有∠APG=90°﹣∠PAG=∠HAQ.
在△AGP和△QHA中,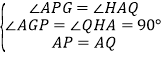 ,∴△AGP≌△QHA,∴PG=AH.
,∴△AGP≌△QHA,∴PG=AH.
∵AH=AO﹣OH=3﹣1=2,∴PG=2,∴yP=2.
解﹣x2﹣2x+3=2得:x1=﹣1![]() ,x2=﹣1
,x2=﹣1![]() .
.
∵点P在第二象限,∴点P的坐标为(﹣1![]() ,2).
,2).
Ⅲ.若AP为等腰直角△APQ的底边,如图4,则有AQ=PQ,∠AQP=90°.
过点P作PT⊥QH,垂足为T,则有∠AQH=90°﹣∠PQT=∠TPQ.
在△AHQ和△QTP中,∵∠AQH=∠TPQ,∠AHQ=∠QTP,QA=QP,∴△AHQ≌△QTP,∴AH=QT,QH=PT.
∵AH=2,∴QT=2.
设QH=PT=p(p>0),则TH=p+2.
∵点P在第二象限,∴点P的坐标为(﹣p﹣1,p+2).
∵点P在抛物线y=﹣x2﹣2x+3上,∴p+2=﹣(﹣p﹣1)2﹣2×(﹣p﹣1)+3.
整理得:p2+p﹣2=0.
解得:p1=﹣2(舍去),p2=1,∴点P的坐标为(﹣2,3).
综上所述:点P的坐标为(![]() )、(﹣1
)、(﹣1![]() ,2)、(﹣2,3).
,2)、(﹣2,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与半径为2的⊙O相切于点C,点D、E、F是⊙O上三个点,EF//AB,若EF=2
 ,则∠EDC的度数为__________.
,则∠EDC的度数为__________.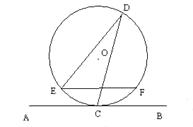
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4 m.按照图中所示的直角坐标系,抛物线可以用y=
 x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为
x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为 m.
m. (1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?

-
科目: 来源: 题型:
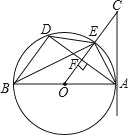
查看答案和解析>>【题目】如图,AB是⊙O的直径,AC切⊙O于点A,AD是⊙O的弦,OC⊥AD于F交⊙O于E,连接DE,BE,BD,AE.
(1)求证:∠C=∠BED;
(2)如果AB=10,tan∠BAD=
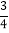 ,求AC的长;
,求AC的长;(3)如果DE∥AB,AB=10,求四边形AEDB的面积.
-
科目: 来源: 题型:
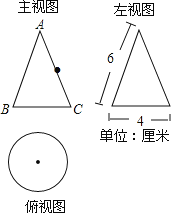
查看答案和解析>>【题目】如图是一个几何体的三视图.
(1)写出该几何体的名称,并根据所示数据计算这个几何体的表面积;
(2)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
-
科目: 来源: 题型:
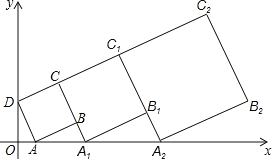
查看答案和解析>>【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,按这样的规律进行下去,第2011个正方形(正方形ABCD看作第1个)的面积为( )
A.5(
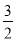 )2010 B.5(
)2010 B.5(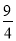 )2010 C.5(
)2010 C.5(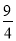 )2011 D.5(
)2011 D.5(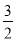 )2011
)2011 -
科目: 来源: 题型:
查看答案和解析>>【题目】若实数 m、n 满足m+n=mn,且n≠0时,就称点 P(m,
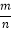 )为“完美点”,若反比例函数y=
)为“完美点”,若反比例函数y=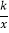 的图象上存在两个“完美点”A、B,且 AB=4,则 k的值为_____.
的图象上存在两个“完美点”A、B,且 AB=4,则 k的值为_____.
相关试题

