【题目】若实数 m、n 满足m+n=mn,且n≠0时,就称点 P(m,![]() )为“完美点”,若反比例函数y=
)为“完美点”,若反比例函数y=![]() 的图象上存在两个“完美点”A、B,且 AB=4,则 k的值为_____.
的图象上存在两个“完美点”A、B,且 AB=4,则 k的值为_____.
参考答案:
【答案】![]()
【解析】
首先得出完美点所在的函数解析式,进而利用韦达定理求出k的值,进而得出答案.
∵m+n=mn且n≠0,
∴![]() +1=m,即
+1=m,即![]() =m-1,
=m-1,
∴P(m,m-1),
即“完美点”P在直线y=x-1上,设点A、B坐标分别为(x1,y1),(x2,y2),
令![]() =x-1化简得x2-x-k=0,
=x-1化简得x2-x-k=0,
∵AB=4,
∴|x1-x2|=2![]() ,
,
由根与系数的关系得x1+x2=1,x1x2=-k,
∴(x1-x2)2=(x1+x2)2-4x1x2=8,
∴1+4k=8,
解得:k=![]() ,
,
此时x2-x-k=0的△>0,
∴k=![]() ;
;
故答案为:![]() .
.
-
科目: 来源: 题型:
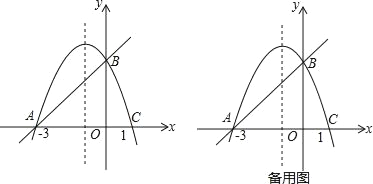
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c经过A、B、C三点,已知点A(﹣3,0),B(0,m),C(1,0).
(1)求m值;
(2)设点P是直线AB上方的抛物线上一动点(不与点A、B重合).
①过点P作x轴的垂线,垂足为F,交直线AB于点E,作PD⊥AB于点D.动点P在什么位置时,△PDE的周长最大,求出此时P点的坐标;
②连接AP,并以AP为边作等腰直角△APQ,当顶点Q恰好落在抛物线的对称轴上时,求出对应的点P坐标.
-
科目: 来源: 题型:
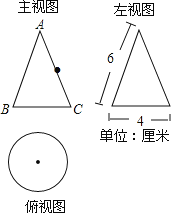
查看答案和解析>>【题目】如图是一个几何体的三视图.
(1)写出该几何体的名称,并根据所示数据计算这个几何体的表面积;
(2)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
-
科目: 来源: 题型:
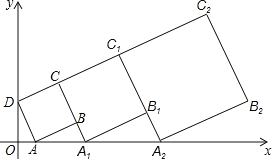
查看答案和解析>>【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,按这样的规律进行下去,第2011个正方形(正方形ABCD看作第1个)的面积为( )
A.5(
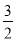 )2010 B.5(
)2010 B.5(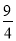 )2010 C.5(
)2010 C.5(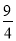 )2011 D.5(
)2011 D.5(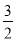 )2011
)2011 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动;同时,点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动.当点P移动到点A时,P、Q同时停止移动.设点P出发xs时,△PAQ的面积为ycm2,y与x的函数图象如图②,则线段EF所在的直线对应的函数关系式为 .
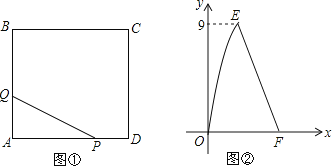
-
科目: 来源: 题型:
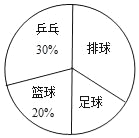
查看答案和解析>>【题目】某校为了调查八年级学生参加“乒乓”、“篮球”、“足球”、“排球”四项体育活动的人数,学校从八年级随机抽取了部分学生进行调查,根据调查结果制作了如下不完整的统计表、统计图:
类别
频数(人数)
频率
乒乓
a
0.3
篮球
20
足球
15
b
排球
合计
c
1
请你根据以上信息解答下列各题:
(1)a= ;b= ;c= ;
(2)在扇形统计图中,排球所对应的圆心角是 度;
(3)若该校八年级共有600名学生,试估计该校八年级喜欢足球的人数?.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交与点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.
(1)求证:∠BCP=∠BAN.
(2)若AC=4,PC=3,求MNBC的值.

相关试题

