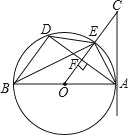
【题目】如图,AB是⊙O的直径,AC切⊙O于点A,AD是⊙O的弦,OC⊥AD于F交⊙O于E,连接DE,BE,BD,AE.
(1)求证:∠C=∠BED;
(2)如果AB=10,tan∠BAD=![]() ,求AC的长;
,求AC的长;
(3)如果DE∥AB,AB=10,求四边形AEDB的面积.
参考答案:
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据切线性质、垂直的性质、直角三角形的两个锐角互余的性质求得∠C+∠AOC=∠AOC+∠BAD=90°,即∠C=∠BAD;然后由圆周角定理推知∠BED=∠BAD;最后由等量代换证得∠C=∠BED;
(2)根据锐角三角函数的定义求AC的长;
(3)根据已知条件推知AE=BD=DE,然后由圆的弧、弦、圆心角间的关系知![]() ,从而求得∠BAD=30°;然后由直径AB所对的圆周角∠ADB=90°可以求得直角三角形ABD中30°所对的直角边是斜边的一半BD
,从而求得∠BAD=30°;然后由直径AB所对的圆周角∠ADB=90°可以求得直角三角形ABD中30°所对的直角边是斜边的一半BD![]() AB=5,DE=5;最后(过点D作DH⊥AB于H)在直角三角形HDA中求得高线DH的长度,从而求得梯形ABDE的面积.
AB=5,DE=5;最后(过点D作DH⊥AB于H)在直角三角形HDA中求得高线DH的长度,从而求得梯形ABDE的面积.
(1)∵AB是⊙O的直径,CA切⊙O于A,∴∠C+∠AOC=90°;
又∵OC⊥AD,∴∠OFA=90°,∴∠AOC+∠BAD=90°,∴∠C=∠BAD.
又∵∠BED=∠BAD,∴∠C=∠BED.
(2)由(1)知∠C=∠BAD,tan∠BAD![]() ,∴tan∠C
,∴tan∠C![]() .
.
在Rt△OAC中,tan∠C![]() ,且OA
,且OA![]() AB=5,∴
AB=5,∴![]() ,解得:
,解得:![]() .
.
(3)∵OC⊥AD,∴![]() ,∴AE=ED.
,∴AE=ED.
又∵DE∥AB,∴∠BAD=∠EDA,∴![]() ,∴AE=BD,∴AE=BD=DE,∴
,∴AE=BD,∴AE=BD=DE,∴![]() ,∴∠BAD=30°.
,∴∠BAD=30°.
又∵AB是直径,∴∠ADB=90°,∴BD![]() AB=5,DE=5.在Rt△ABD中,由勾股定理得:AD
AB=5,DE=5.在Rt△ABD中,由勾股定理得:AD![]() ,过点D作DH⊥AB于H.
,过点D作DH⊥AB于H.
∵∠HAD=30°,∴DH![]() AD
AD![]() ,∴四边形AEDB的面积
,∴四边形AEDB的面积![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(问题情境)如图
 ,
,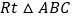 中,
中,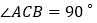 ,
,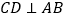 ,我们可以利用
,我们可以利用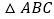 与
与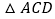 相似证明
相似证明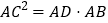 ,这个结论我们称之为射影定理,试证明这个定理;
,这个结论我们称之为射影定理,试证明这个定理;(结论运用)如图
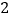 ,正方形
,正方形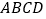 的边长为
的边长为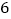 ,点
,点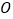 是对角线
是对角线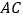 、
、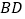 的交点,点
的交点,点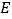 在
在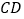 上,过点
上,过点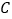 作
作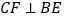 ,垂足为
,垂足为 ,连接
,连接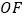 ,
, (1)试利用射影定理证明
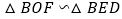 ;
;(2)若
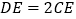 ,求
,求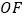 的长.
的长.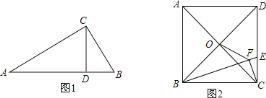
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与半径为2的⊙O相切于点C,点D、E、F是⊙O上三个点,EF//AB,若EF=2
 ,则∠EDC的度数为__________.
,则∠EDC的度数为__________.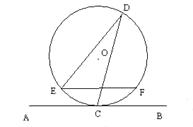
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4 m.按照图中所示的直角坐标系,抛物线可以用y=
 x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为
x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为 m.
m. (1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?

-
科目: 来源: 题型:
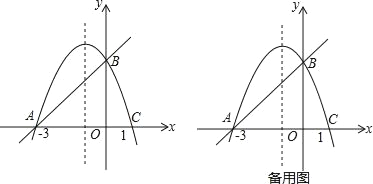
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c经过A、B、C三点,已知点A(﹣3,0),B(0,m),C(1,0).
(1)求m值;
(2)设点P是直线AB上方的抛物线上一动点(不与点A、B重合).
①过点P作x轴的垂线,垂足为F,交直线AB于点E,作PD⊥AB于点D.动点P在什么位置时,△PDE的周长最大,求出此时P点的坐标;
②连接AP,并以AP为边作等腰直角△APQ,当顶点Q恰好落在抛物线的对称轴上时,求出对应的点P坐标.
-
科目: 来源: 题型:
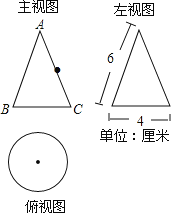
查看答案和解析>>【题目】如图是一个几何体的三视图.
(1)写出该几何体的名称,并根据所示数据计算这个几何体的表面积;
(2)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
-
科目: 来源: 题型:
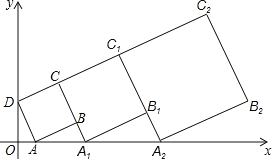
查看答案和解析>>【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,按这样的规律进行下去,第2011个正方形(正方形ABCD看作第1个)的面积为( )
A.5(
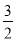 )2010 B.5(
)2010 B.5(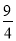 )2010 C.5(
)2010 C.5(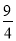 )2011 D.5(
)2011 D.5(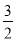 )2011
)2011
相关试题

