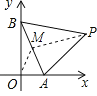
【题目】如图,点P在第一象限,△ABP是边长为2的等边三角形,当点A在x轴的正半轴上运动时,点B随之在y轴的正半轴上运动,运动过程中,点P到原点的最大距离是______;若将△ABP的PA边长改为![]() ,另两边长度不变,则点P到原点的最大距离变为______.
,另两边长度不变,则点P到原点的最大距离变为______.

参考答案:
【答案】1+![]() 1+
1+![]()
【解析】
根据当O到AB的距离最大时,OP的值最大,得到O到AB的最大值是![]() AB=1,此时在斜边的中点M上,由勾股定理求出PM,即可求出答案;将△ABP的PA边长改为
AB=1,此时在斜边的中点M上,由勾股定理求出PM,即可求出答案;将△ABP的PA边长改为![]() ,另两边长度不变,根据
,另两边长度不变,根据![]() ,得到∠PBA=90°,由勾股定理求出PM即可.
,得到∠PBA=90°,由勾股定理求出PM即可.
取AB的中点M,连OM,PM,
在Rt△ABO中,OM=![]() =1,在等边三角形ABP中,PM=
=1,在等边三角形ABP中,PM=![]() ,
,
无论△ABP如何运动,OM和PM的大小不变,当OM,PM在一直线上时,P距O最远,
∵O到AB的最大值是![]() AB=1,此时在斜边的中点M上, 由勾股定理得:PM=
AB=1,此时在斜边的中点M上, 由勾股定理得:PM=![]() ,
,
∴OP=1+![]() ,
,
将△AOP的PA边长改为![]() ,另两边长度不变, ∵
,另两边长度不变, ∵![]() ,
,
∴∠PBA=90°,由勾股定理得:PM=![]() , ∴此时OP=OM+PM=1+
, ∴此时OP=OM+PM=1+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边的中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边的中点,得到四边形A2B2C2D2;…;如此进行下去,得到四边形A7B7C7D7,那么四边A7B7C7D7形的周长为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣4,﹣3,1,3,4这五个数中,随机抽取一个数,记为m,若m使得关于x,y的二元一次方程组
 有解,且使关于x的分式方程
有解,且使关于x的分式方程  ﹣1=
﹣1=  有正数解,那么这五个数中所有满足条件的m的值之和是( )
有正数解,那么这五个数中所有满足条件的m的值之和是( )
A.1
B.2
C.﹣1
D.﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在正方形ABCD中,F是CD边上一点(不和C,D重合),过点D做DG⊥BF交BF延长线于点G.连接AG,交BD于点E,连接EF,交CD于点M.若DG=6,AG=7
 ,则EF的长为 .
,则EF的长为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为
 ,C点的坐标为
,C点的坐标为 ,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着
,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着 的路线移动
的路线移动 即:沿着长方形移动一周
即:沿着长方形移动一周 .
. 写出点B的坐标
写出点B的坐标 ______
______
 当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标. 在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
(1)描出A(﹣4,3)、B(﹣1,0)、C(﹣2,3)三点.
(2)△ABC 的面积是多少?
(3)作出△ABC 关于 y 轴的对称图形.
(4)请在x 轴上求作一点P,使△PA1C1 的周长最小,并直接写出点P 的坐标

-
科目: 来源: 题型:
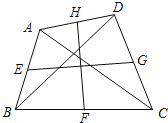
查看答案和解析>>【题目】如图,在四边形ABCD中,AC=BD=6,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2=______.
相关试题

