【题目】如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边的中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边的中点,得到四边形A2B2C2D2;…;如此进行下去,得到四边形A7B7C7D7,那么四边A7B7C7D7形的周长为______.

参考答案:
【答案】![]()
【解析】
根据三角形中位线性质定理可得每一次取各边中点,所形成的新四边形周长都为前一个的![]() ;并且四边形是平行四边形,即可计算四边A7B7C7D7形的周长,
;并且四边形是平行四边形,即可计算四边A7B7C7D7形的周长,
解:∵在四边形ABCD中,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,
∴A1D1∥BD,B1C1∥BD,C1D1∥AC,A1B1∥AC;
∴A1D1∥B1C1,A1B1∥C1D1,
∴四边形A1B1C1D1是平行四边形;
同理,四边形A7B7C7D7是平行四边形;
根据中位线的性质知,A7B7=![]() A5B5;A5B5=
A5B5;A5B5=![]() A3B3;A3B3=
A3B3;A3B3=![]() A1B1;A1B1=
A1B1;A1B1=![]() AC;
AC;
故可得A7B7=![]() ×
×![]() ×
×![]() ×
×![]() AC=
AC=![]() ;
;
同理可得:B7C7=![]() ;
;
故四边形A7B7C7D7的周长是2×![]() =
=![]() .
.
故答案为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:


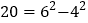
因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为
 和
和 (其中
(其中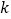 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由. (3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )

A. 若AD⊥BC,则四边形AEDF是矩形
B. 若AD垂直平分BC,则四边形AEDF是矩形
C. 若BD=CD,则四边形AEDF是菱形
D. 若AD平分∠BAC,则四边形AEDF是菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,M是BC边的中点,AP平分∠A,BP⊥AP于点P、若AB=12,AC=22,则MP的长为_________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣4,﹣3,1,3,4这五个数中,随机抽取一个数,记为m,若m使得关于x,y的二元一次方程组
 有解,且使关于x的分式方程
有解,且使关于x的分式方程  ﹣1=
﹣1=  有正数解,那么这五个数中所有满足条件的m的值之和是( )
有正数解,那么这五个数中所有满足条件的m的值之和是( )
A.1
B.2
C.﹣1
D.﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在正方形ABCD中,F是CD边上一点(不和C,D重合),过点D做DG⊥BF交BF延长线于点G.连接AG,交BD于点E,连接EF,交CD于点M.若DG=6,AG=7
 ,则EF的长为 .
,则EF的长为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P在第一象限,△ABP是边长为2的等边三角形,当点A在x轴的正半轴上运动时,点B随之在y轴的正半轴上运动,运动过程中,点P到原点的最大距离是______;若将△ABP的PA边长改为
 ,另两边长度不变,则点P到原点的最大距离变为______.
,另两边长度不变,则点P到原点的最大距离变为______.
相关试题

