【题目】如图,在平面直角坐标系中,
(1)描出A(﹣4,3)、B(﹣1,0)、C(﹣2,3)三点.
(2)△ABC 的面积是多少?
(3)作出△ABC 关于 y 轴的对称图形.
(4)请在x 轴上求作一点P,使△PA1C1 的周长最小,并直接写出点P 的坐标

参考答案:
【答案】(1)描点见解析;(2)3;(3)作图见解析;(4)见解析,点P的坐标为(3,0).
【解析】
利用A,B,C各点坐标在平面坐标系中描出即可;
利用三角形面积公式求出即可;
利用关于y轴对称点的坐标性质进而得出答案.
利用轴对称求最短路线的方法得出P点位置.
(1)如图所示:△ABC即为所求;
(2)△ABC的面积是:![]() ×2×3=3;
×2×3=3;
(3)如图所示:△A1B1C1即为所求;
(4)如图所示,作点A1关于y轴的对称点Q,连接C1Q,交x轴于点P,则C1P=A1P,
∴△PA1C1的周长最小值为A1C1+C1Q的长,此时点P的坐标为(3,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在正方形ABCD中,F是CD边上一点(不和C,D重合),过点D做DG⊥BF交BF延长线于点G.连接AG,交BD于点E,连接EF,交CD于点M.若DG=6,AG=7
 ,则EF的长为 .
,则EF的长为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P在第一象限,△ABP是边长为2的等边三角形,当点A在x轴的正半轴上运动时,点B随之在y轴的正半轴上运动,运动过程中,点P到原点的最大距离是______;若将△ABP的PA边长改为
 ,另两边长度不变,则点P到原点的最大距离变为______.
,另两边长度不变,则点P到原点的最大距离变为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为
 ,C点的坐标为
,C点的坐标为 ,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着
,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着 的路线移动
的路线移动 即:沿着长方形移动一周
即:沿着长方形移动一周 .
. 写出点B的坐标
写出点B的坐标 ______
______
 当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标. 在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
-
科目: 来源: 题型:
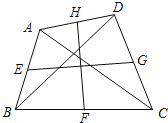
查看答案和解析>>【题目】如图,在四边形ABCD中,AC=BD=6,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】长为5,宽为
 的长方形纸片(
的长方形纸片( ),如图那样翻折,剪下一个边长等于长方形宽度的正方形(成为第一次操作);再把剩下的长方形如图那样翻折,剪下一个边长等于此时长方形宽度的正方形(称为第二次操作);若在第3次操作后,剩下的图形为正方形,则
),如图那样翻折,剪下一个边长等于长方形宽度的正方形(成为第一次操作);再把剩下的长方形如图那样翻折,剪下一个边长等于此时长方形宽度的正方形(称为第二次操作);若在第3次操作后,剩下的图形为正方形,则 的值为__________.
的值为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=∠B=50°,P 为 AB 中点,点 M 为射线 AC 上(不与点 A 重合)的任意一点,连接 MP, 并使MP 的延长线交射线BD 于点N,设∠BPN=α.

(1)求证:△APM≌△BPN;
(2)当 MN=2BN 时,求α的度数;
(3)若△BPN 为锐角三角形时,直接写出α的取值范围.
相关试题

