【题目】如图,线段AB=24,动点P从A出发,以每秒2个单位的速度沿射线AB运动,运动时间为t秒(t>0),点M为AP的中点.
![]()
(1)当点P在线段AB上运动时.当t为多少时,AM=6.
(2)当点P在AB延长线上运动时,点N为BP的中点,求出线段MN的长度.
(3)在P点的运动过程中,点N为BP的中点,是否存在这样的t的值,使M、N、B三点中的一个点是以其余两点为端点的线段的中点,若有,请求出t的值;若没有,请说明理由.
参考答案:
【答案】(1)t=6;(2)12;(3)当t=18时,M是线段AP的中点;当t=36时,M为BN的中点,理由见解析.
【解析】
(1)根据AM=![]() AP即可求解;
AP即可求解;
(2)由M是线段AP的中点,可求PM=![]() AP=t,由N是线段BP的中点,可求PN=
AP=t,由N是线段BP的中点,可求PN=![]() BP=t-12,把二者相加即可求出MN的值;
BP=t-12,把二者相加即可求出MN的值;
(3)分N为BP的中点,B为MN的中点,M为BN的中点三种情况讨论求解.
解:(1)∵M是线段AP的中点,
∴AM=![]() AP=t,
AP=t,
∵AM=6,
∴t=6;
(2)点P在AB延长线上运动时,
∵M是线段AP的中点,
∴PM=![]() AP=t,
AP=t,
∵N是线段BP的中点,
∴PN=![]() BP=
BP=![]() (2t-24)=t-12.
(2t-24)=t-12.
∴MN=t-(t-12)=12.
(3)当0<t≤12,
∵N为BP的中点,
∴此时不符合题意;
当12<t≤48,B为MN的中点时,
![]()
∵N为BP的中点时,
∴BN=PN=![]() PB=t-12,
PB=t-12,
∵M是线段AP的中点,
∴AM=PM=![]() AP=t,
AP=t,
∴BM=24-t,
∴24-t=t-12,
∴t=18;
当t>48,M为BN的中点时,
![]()
由题意得:
BN=NP=t-12,AM=PM=t,
∴BM=t-24,MN=t-(t-12)=12,
∴t-24=12,
∴t=36.
∴当t=18时,M是线段AP的中点;当t=36时,M为BN的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店老板第一次用1000元购进一批文具,很快销售完毕,第二次购进时发现每件文具的进价比第一次上涨了2.5元,老板用2500元购进了第二批文具,所购进文具的数量是第一次购进数量的2倍,同样很快销售完毕,已知两批文具的售价均为每件15元.
(1)第二次购进了多少件文具?
(2)文具店老板在这两笔生意中共盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某水库养殖鱼的有关情况,从该水库多个不同位置捕捞出200条鱼,称得每条鱼的质量(单位:千克),并将所得数据分组,绘制了直方图
(1)根据直方图提供的信息,这组数据的中位数落在________范围内.
(2)估计数据落在1.00~1.15中的频率是________.
(3)将上面捕捞的200条鱼分别作一记号后再放回水库.几天后再从水库的多处不同的位置捕捞150条鱼,其中带有记号的鱼有10条,请根据这一情况估算该水库中鱼的总条数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某大学生利用业余时间参与了一家网店经营,销售一种成本为30元/件的文化衫,根据以往的销售经验,他整理出这种文化衫的售价y1(元/件),销量y2(件)与第x(1≤x<90)天的函数图象如图所示(销售利润=(售价-成本)×销量).
(1)求y1与y2的函数解析式.
(2)求每天的销售利润W与x的函数解析式.
(3)销售这种文化衫的第多少天,销售利润最大,最大利润是多少?


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知△ABC中,AB=BC=1,∠ABC=90°,把一块含30°角的直角三角板DEF的直角顶点D放在AC的中点上(直角三角板的短直角边为DE,长直角边为DF),将直角三角板DEF绕D点按逆时针方向旋转.
(1)在图1中,DE交AB于M,DF交BC于N.
①求证:DM=DN;
②在这一旋转过程中,直角三角板DEF与△ABC的重叠部分为四边形DMBN,请说明四边形DMBN的面积是否发生变化?若发生变化,请说明是如何变化的?若不发生变化,求出其面积;
(2)继续旋转至如图2的位置,延长AB交DE于M,延长BC交DF于N,DM=DN是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(3)继续旋转至如图3的位置,延长FD交BC于N,延长ED交AB于M,DM=DN是否仍然成立?请写出结论,不用证明.

-
科目: 来源: 题型:
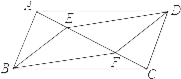
查看答案和解析>>【题目】如图,E、F是ABCD对角线AC上两点,且AE=CF.
(1)求证:四边形BFDE是平行四边形.
(2)如果把条件AE=CF改为BE=DF,试问四边形BFDE还是平行四边形吗?为什么?
-
科目: 来源: 题型:
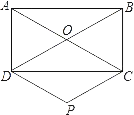
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,过点C,D分别作BD,AC的平行线,两线相交于点P.
(1)求证:四边形CODP是菱形;
(2)当矩形ABCD的边AD,DC满足什么关系时,菱形CODP是正方形?请说明理由.
相关试题

