【题目】乘法公式的探究及应用.
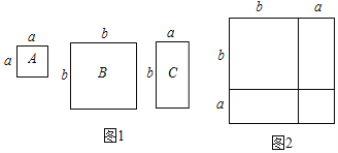
数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积.方法1:______;方法2:_______.
(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系._______;
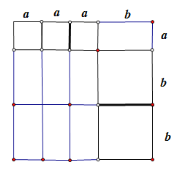
(3)类似的,请你用图1中的三种纸片拼一个使长方形面积为:3a2+7ab+2b2,并对3a2+7ab+2b2因式分解为_______.
(4)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(x﹣2016)2+(x﹣2018)2=34,求(x﹣2017)2的值.
参考答案:
【答案】(1)(a+b)2;a2+b2+2ab;(2)(a+b)2=a2+2ab+b2;(3)3a2+7ab+2b2=(a+2b)(3a+b);(4)①ab=7;②(x﹣2017)2=16.
【解析】
(1)直接利用大正方形的边长×边长;将所有的小正方形与矩形的面积相加;
(2)根据(1)与大正方形的面积不变即可得解;
(3)根据题意画出图形,再利用面积相等的列出等式即可;
(4)①根据题意将a+b平方,利用完全平方公式变形求解即可;
②利用完全平方公式去括号将原式变为2(x2﹣2×2017x+20172)+20182+20162﹣2×20172=34,再利用平方差公式变形求解即可.
解:(1)大正方形的边长为a+b,则其面积为(a+b)2;
两个小正方形的面积为a2,b2,长方形的面积为2ab,则其面积为a2+b2+2ab;
(2)根据大正方形的面积相等得:(a+b)2=a2+2ab+b2;
(3)如图,可得3a2+7ab+2b2=(a+2b)(3a+b);
(4)①(a+b)2= a2+2ab+b2=25,
∵a2+b2=11,
∴2ab=14,
解得ab=7;
②∵(x﹣2016)2+(x﹣2018)2=34,
∴x2﹣2×2016x+20162+x2﹣2×2018x+20182=34,
∴2(x2﹣2×2017x+20172)+20182+20162﹣2×20172=34,
∴2(x﹣2017)2+2018+2017﹣2016﹣2017=34,
则(x﹣2017)2=16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】坐火车从上海到娄底,高铁G1329次列车比快车K575次列车少要9小时,已知上海到娄底的铁路长约1260千米,G1329的平均速度是K575的2.5倍.
(1)求K575的平均速度;
(2)高铁G1329从上海到娄底只需几小时? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,矩形ABCD的边AD=3,A(
 ,0),B(2,0),直线y=kx+b经过B,D两点.
,0),B(2,0),直线y=kx+b经过B,D两点.(1)求直线y=kx+b的解析式;
(2)将直线y=kx+b平移,若它与矩形有公共点,直接写出b的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,各内角的平分线分别相交于点E,F,G,H.
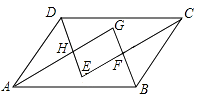
(1)求证:△ABG≌△CDE;
(2)猜一猜:四边形EFGH是什么样的特殊四边形?证明你的猜想;
(3)若AB=6,BC=4,∠DAB=60°,求四边形EFGH的面积. -
科目: 来源: 题型:
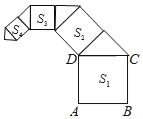
查看答案和解析>>【题目】如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S2018的值为( )
A.
 B.
B. 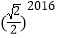 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】王老师家买了一套新房,其结构如图所示(单位:m).他打算将卧室铺上木地板,其余部分铺上地砖.
(1)木地板和地砖分别需要多少平方米?
(2)如果地砖的价格为每平方米x元,木地板的价格为每平方米3x元,那么王老师需要花多少钱?

-
科目: 来源: 题型:
查看答案和解析>>【题目】去冬今春,某市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来.
相关试题

