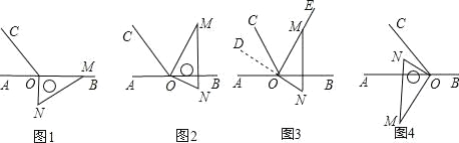
【题目】已知,在下列各图中,点 O 为直线 AB 上一点,∠AOC=60°,直角三角板的直角顶点放在点处.
(1)如图 1,三角板一边 OM在射线 OB 上,另一边 ON在直线 AB的下方,求∠BOC的度数,∠CON 的度数;
(2)如图 2,三角板一边OM恰好在∠BOC的角平分线OE上,另一边ON在直线 AB的下方,求此时∠BON 的度数;
(3)请从下列(A),(B)两题中任选一题作答. 我选择哪一题.
(A)在图 2 中,延长线段 NO 得到射线 OD,如图 3,求∠AOD 的度数;写出∠DOC 与∠BON 的数量关系;
(B)如图 4,MN⊥AB,ON 在∠AOC 的内部,若另一边 OM 在直线 AB 的下方, 求∠COM+∠AON 的度数;∠AOM﹣∠CON 的度数.
参考答案:
【答案】(1)120;150;(2)30°;(3)A(或 B);(A)30;∠DOC=∠BON;(B)150;30.
【解析】
(1)利用两角互补,即可得出结论;
(2)根据OM平分∠BOC,可得出∠BOM=60°,由∠MON=∠BOM+∠BON=90°可求得∠BON的度数;
(3)根据直角三角板MON各角的度数以及图中各角的关系即能得出结论.
(1)∵∠AOC=60°,∠BOC 与∠AOC 互补,∠AON=90°
∴∠BOC=180°﹣60°=120°,∠CON=∠AOC+∠AON=60°+90°=150°.
(2)∵三角板一边 OM 恰好在∠BOC 的角平分线 OE 上,∠BOC=120°,
∴∠BOM= ![]() ∠BOC=60°,
∠BOC=60°,
又∵∠MON=∠BOM+∠BON=90°,
∴∠BON=90°﹣60°=30°.
(3)(A)∵∠AOD=∠BON(对顶角),∠BON=30°,
∴∠AOD=30°, 又∵∠AOC=60°,
∴∠DOC=∠AOC﹣∠AOD=60°﹣30°=30°=∠BON.
(B)∵MN⊥AB,
∴∠AON 与∠MNO 互余,
∵∠MNO=60°(三角板里面的 60°角),
∴∠AON=90°﹣60°=30°,
∵∠AOC=60°,150
∴∠CON=∠AOC﹣∠AON=60°﹣30°=30°,
∴∠COM+∠AON=∠MON+2∠CON=90°+2×30°=150°,
∠AOM﹣∠CON=∠MON﹣2∠CON=90°﹣2×30°=30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知∠ABC=90°,△ABC是等腰三角形,点D为斜边AC的中点,连接DB,过点A作∠BAC的平分线,分别与DB,BC相交于点E,F.
(1)求证:BE=BF;
(2)如图2,连接CE,在不添加任何辅助线的条件下,直接写出图中所有的等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AD的延长线相交于点F,且AD=3,cos∠BCD=
 .
. 
(1)求证:CD∥BF;
(2)求⊙O的半径;
(3)求弦CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)某中学组织学生去福利院慰问,在准备礼品时发现,购买1个甲礼品比购买1个乙礼品多花40元,并且花费600元购买甲礼品和花费360元购买乙礼品的数量相等.
(1)求甲、乙两种礼品的单价各为多少元?
(2)学校准备购买甲、乙两种礼品共30个送给福利院的老人,要求购买礼品的总费用不超过2000元,那么最多可购买多少个甲礼品?
-
科目: 来源: 题型:
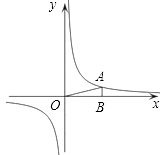
查看答案和解析>>【题目】如图,在直角坐标系中,O为坐标原点.已知反比例函数y=
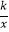 (k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为
(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为  .
.
(1)求k和m的值;
(2)点C(x,y)在反比例函数y=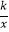 的图象上,求当1≤x≤3时函数值y的取值范围;
的图象上,求当1≤x≤3时函数值y的取值范围;
(3)过原点O的直线l与反比例函数y=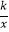 的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值.
的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O是坐标原点,点B(0,12),点A在第一象限内,△AOB为等腰三角形,∠BAO=90°,AB=AO,AC⊥OB,点D从点B出发,以每秒2个单位的速度沿y轴向终点O运动,连接DA,过点A作AE⊥AD,射线AE交x轴于点E,连接BE,交线段AC于点F,交线段OA于点G.
(1)请直接写出A的坐标;
(2)点D运动的时间为t秒时,用含t的代数式表示△ACD的面积S,并写出t的取值范围;
(3)在(2)的条件下,当四边形DAEO的面积等于6S时,求△AGF的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分)如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.

相关试题

