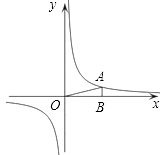
【题目】如图,在直角坐标系中,O为坐标原点.已知反比例函数y= ![]() (k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为
(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为 ![]() .
.
(1)求k和m的值;
(2)点C(x,y)在反比例函数y= ![]() 的图象上,求当1≤x≤3时函数值y的取值范围;
的图象上,求当1≤x≤3时函数值y的取值范围;
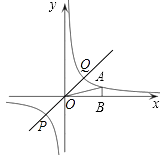
(3)过原点O的直线l与反比例函数y= ![]() 的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值.
的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值.
参考答案:
【答案】
(1)
解:∵A(2,m),
∴OB=2,AB=m,
∴S△AOB= ![]() OBAB=
OBAB= ![]() ×2×m=
×2×m= ![]() ,
,
∴m= ![]() ;
;
∴点A的坐标为(2, ![]() ),
),
把A(2, ![]() )代入y=
)代入y= ![]() ,得
,得 ![]() =
= ![]()
∴k=1;
(2)
解:∵当x=1时,y=1;当x=3时,y= ![]() ,
,
又∵反比例函数y= ![]() ,在x>0时,y随x的增大而减小,
,在x>0时,y随x的增大而减小,
∴当1≤x≤3时,y的取值范围为 ![]() ≤y≤1
≤y≤1
(3)
解:由图象可得:P,Q关于原点对称,
∴PQ=2OP,
反比例函数解析式为y= ![]() ,设P(a,
,设P(a, ![]() ),
),
∴OP= ![]() =
= ![]() ,
,
∴OP最小值为 ![]() ,
,
∴线段PQ长度的最小值为2 ![]() .
.
【解析】(1)根据三角形的面积公式先得到m的值,然后把点A的坐标代入y= ![]() ,可求出k的值;(2)根据反比例函数得性质求解;(3)P,Q关于原点对称,则PQ=2OP,设P(a,
,可求出k的值;(2)根据反比例函数得性质求解;(3)P,Q关于原点对称,则PQ=2OP,设P(a, ![]() ),根据勾股定理得到OP=
),根据勾股定理得到OP= ![]() =
= ![]() ,从而得到OP最小值为
,从而得到OP最小值为 ![]() ,于是可得到线段PQ长度的最小值.
,于是可得到线段PQ长度的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AD的延长线相交于点F,且AD=3,cos∠BCD=
 .
. 
(1)求证:CD∥BF;
(2)求⊙O的半径;
(3)求弦CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)某中学组织学生去福利院慰问,在准备礼品时发现,购买1个甲礼品比购买1个乙礼品多花40元,并且花费600元购买甲礼品和花费360元购买乙礼品的数量相等.
(1)求甲、乙两种礼品的单价各为多少元?
(2)学校准备购买甲、乙两种礼品共30个送给福利院的老人,要求购买礼品的总费用不超过2000元,那么最多可购买多少个甲礼品?
-
科目: 来源: 题型:
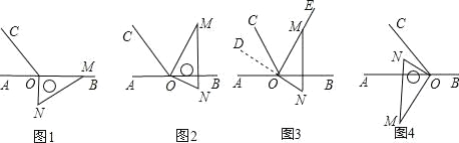
查看答案和解析>>【题目】已知,在下列各图中,点 O 为直线 AB 上一点,∠AOC=60°,直角三角板的直角顶点放在点处.
(1)如图 1,三角板一边 OM在射线 OB 上,另一边 ON在直线 AB的下方,求∠BOC的度数,∠CON 的度数;
(2)如图 2,三角板一边OM恰好在∠BOC的角平分线OE上,另一边ON在直线 AB的下方,求此时∠BON 的度数;
(3)请从下列(A),(B)两题中任选一题作答. 我选择哪一题.
(A)在图 2 中,延长线段 NO 得到射线 OD,如图 3,求∠AOD 的度数;写出∠DOC 与∠BON 的数量关系;
(B)如图 4,MN⊥AB,ON 在∠AOC 的内部,若另一边 OM 在直线 AB 的下方, 求∠COM+∠AON 的度数;∠AOM﹣∠CON 的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O是坐标原点,点B(0,12),点A在第一象限内,△AOB为等腰三角形,∠BAO=90°,AB=AO,AC⊥OB,点D从点B出发,以每秒2个单位的速度沿y轴向终点O运动,连接DA,过点A作AE⊥AD,射线AE交x轴于点E,连接BE,交线段AC于点F,交线段OA于点G.
(1)请直接写出A的坐标;
(2)点D运动的时间为t秒时,用含t的代数式表示△ACD的面积S,并写出t的取值范围;
(3)在(2)的条件下,当四边形DAEO的面积等于6S时,求△AGF的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分)如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】长春外国语学校为了创建全省“最美书屋”,购买了一批图书,其中科普类图书平均每本的价格比文学类图书平均每本的价格多5元.已知学校用12000元购买的科普类图书的本数与用9000元购买的文学类图书的本数相等,求学校购买的科普类图书和文学类图书平均每本的价格各是多少元?
相关试题

